There are objects that are capable of changing the density of the electromagnetic radiation flux falling on them, that is, either increasing it by collecting it at one point, or decreasing it by scattering it. These objects are called lenses in physics. Let's take a closer look at this issue.
What are lenses in physics?
This concept means absolutely any object that is capable of changing the direction of propagation of electromagnetic radiation. This is the general definition of lenses in physics, which includes optical glasses, magnetic and gravitational lenses.
In this article, the focus will be on optical glasses, which are objects made of a transparent material and limited by two surfaces. One of these surfaces must necessarily have curvature (that is, be part of a sphere of finite radius), otherwise the object will not have the property of changing the direction of propagation of light rays.
The principle of the lens

The essence of the work of this uncomplicatedoptical object is the phenomenon of refraction of the sun's rays. At the beginning of the 17th century, the famous Dutch physicist and astronomer Willebrord Snell van Rooyen published the law of refraction, which currently bears his last name. The formulation of this law is as follows: when sunlight passes through the interface between two optically transparent media, then the product of the sine of the angle of incidence between the beam and the normal to the surface and the refractive index of the medium in which it propagates is a constant value.

To clarify the above, let's give an example: let the light fall on the surface of the water, while the angle between the normal to the surface and the beam is θ1. Then, the light beam is refracted and begins its propagation in the water already at an angle θ2 to the normal to the surface. According to Snell's law, we get: sin(θ1)n1=sin(θ2) n2, where n1 and n2 are the refractive indices for air and water, respectively. What is the refractive index? This is a value showing how many times the speed of propagation of electromagnetic waves in vacuum is greater than that for an optically transparent medium, that is, n=c/v, where c and v are the speeds of light in vacuum and in the medium, respectively.
The physics of the appearance of refraction lies in the implementation of Fermat's principle, according to which light moves in such a way as to overcome the distance from one point to another in space in the shortest time.
Types of lenses

The type of optical lens in physics is determined solely by the shape of the surfaces that form it. The direction of refraction of the beam incident on them depends on this shape. So, if the curvature of the surface is positive (convex), then, upon exiting the lens, the light beam will propagate closer to its optical axis (see below). Conversely, if the curvature of the surface is negative (concave), then passing through the optical glass, the beam will move away from its central axis.
Note again that a surface of any curvature refracts rays in the same way (according to Stella's law), but the normals to them have a different slope relative to the optical axis, resulting in different behavior of the refracted ray.
A lens bounded by two convex surfaces is called a converging lens. In turn, if it is formed by two surfaces with negative curvature, then it is called scattering. All other types of optical glasses are associated with a combination of these surfaces, to which a plane is also added. What property the combined lens will have (divergent or converging) depends on the total curvature of the radii of its surfaces.
Lens elements and ray properties

To build in lenses in image physics, you need to get acquainted with the elements of this object. They are listed below:
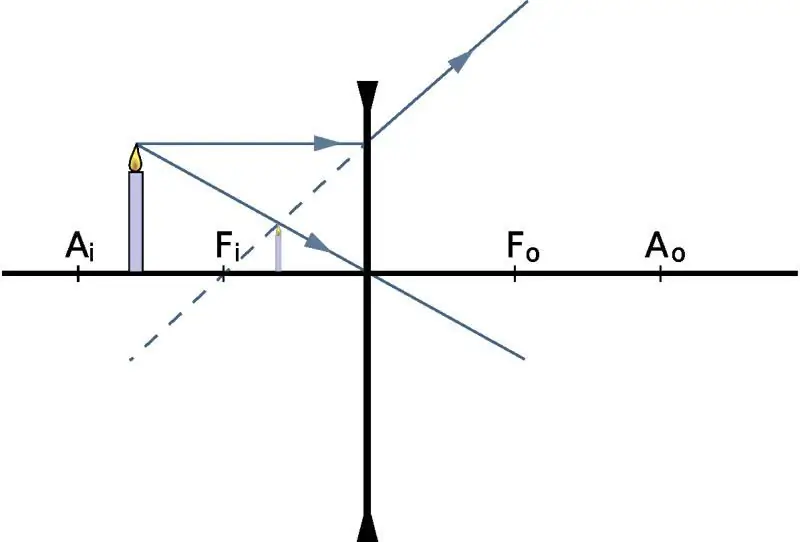
- Main optical axis and center. In the first case, they mean a straight line passing perpendicular to the lens through its optical center. The latter, in turn, is a point inside the lens, passing through which the beam does not experience refraction.
- Focal length and focus - the distance between the center and a point on the optical axis, which collects all the rays incident on the lens parallel to this axis. This definition is true for collecting optical glasses. In the case of divergent lenses, it is not the rays themselves that will converge to a point, but their imaginary continuation. This point is called the main focus.
- Optical power. This is the name of the reciprocal of the focal length, that is, D \u003d 1 / f. It is measured in diopters (diopters), that is, 1 diopter.=1 m-1.
The following are the main properties of the rays that pass through the lens:
- beam passing through the optical center does not change its direction of motion;
- rays incident parallel to the main optical axis change their direction so that they pass through the main focus;
- rays falling on optical glass at any angle, but passing through its focus, change their direction of propagation in such a way that they become parallel to the main optical axis.
The above properties of rays for thin lenses in physics (as they are called because no matter what spheres they are formed and how thick they are, only the optical properties of the object matter) are used to build images in them.
Images in optical glasses: how to build?
Below is a figure that details the schemes for constructing images in the convex and concave lenses of an object(red arrow) depending on its position.
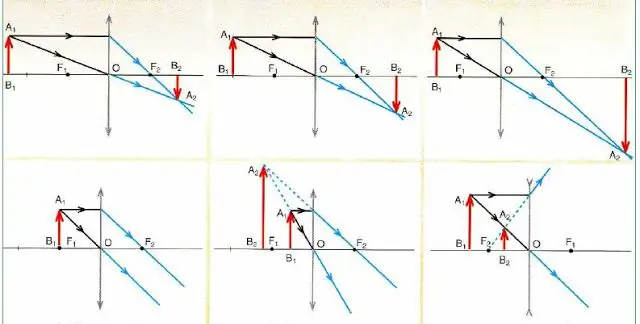
Important conclusions follow from the analysis of the circuits in the figure:
- Any image is built on only 2 rays (passing through the center and parallel to the main optical axis).
- Converging lenses (denoted with arrows at the ends pointing outward) can give both an enlarged and reduced image, which in turn can be real (real) or imaginary.
- If the object is in focus, then the lens does not form its image (see the lower diagram on the left in the figure).
- Scattering optical glasses (denoted by arrows at their ends pointing inward) always give a reduced and virtual image regardless of the position of the object.
Finding the distance to an image
To determine at what distance the image will appear, knowing the position of the object itself, we give the lens formula in physics: 1/f=1/do + 1/d i, where do and di are the distance to the object and to its image from the optical center, respectively, f is the main focus. If we are talking about collecting optical glass, then the f-number will be positive. Conversely, for a diverging lens, f is negative.
Let's use this formula and solve a simple problem: let the object be at a distance do=2f from the center of the collecting optical glass. Where will his image appear?
From the condition of the problem we have: 1/f=1/(2f)+1/di. From: 1/di=1/f - 1/(2f)=1/(2f), i.e. di=2f. Thus, the image will appear at a distance of two foci from the lens, but on the other side than the object itself (this is indicated by the positive sign of the value di).
A Brief History
It is curious to give the etymology of the word "lens". It comes from the Latin words lens and lentis, which means "lentil", since optical objects in their shape really look like the fruit of this plant.
The refractive power of spherical transparent bodies was known to the ancient Romans. For this purpose, they used round glass vessels filled with water. Glass lenses themselves began to be made only in the 13th century in Europe. They were used as a reading tool (modern glasses or a magnifying glass).
The active use of optical objects in the manufacture of telescopes and microscopes dates back to the 17th century (at the beginning of this century, Galileo invented the first telescope). Note that the mathematical formulation of Stella's law of refraction, without knowledge of which it is impossible to manufacture lenses with desired properties, was published by a Dutch scientist at the beginning of the same 17th century.
Other lenses
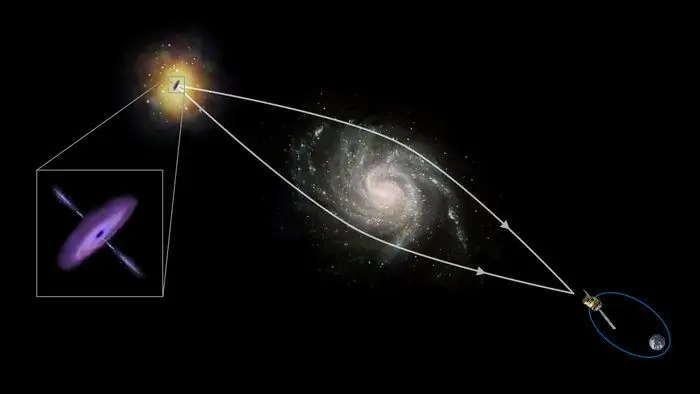
As noted above, in addition to optical refractive objects, there are also magnetic and gravitational objects. An example of the former are magnetic lenses in an electron microscope, a vivid example of the latter is the distortion of the direction of the light flux,when it passes near massive space bodies (stars, planets).






