Each of us threw stones into the sky and watched the trajectory of their fall. This is the most common example of the motion of a rigid body in the field of gravitational forces of our planet. In this article, we will consider formulas that can be useful for solving problems on the free movement of a body thrown to the horizon at an angle.
The concept of moving towards the horizon at an angle
When some solid object is given an initial speed, and it begins to gain height, and then, again, fall to the ground, it is generally accepted that the body moves along a parabolic trajectory. In fact, the solution of equations for this type of motion shows that the line described by the body in the air is part of an ellipse. However, for practical use, the parabolic approximation turns out to be quite convenient and leads to exact results.
Examples of the movement of a body thrown at an angle to the horizon are the firing of a projectile from the muzzle of a cannon, kicking a ball, and even jumping pebbles on the surface of the water ("toads"), which are heldinternational competitions.
The type of movement at an angle is studied by ballistics.
Properties of the considered movement type
When considering the trajectory of a body in the field of the Earth's gravitational forces, the following statements are true:
- knowing the initial height, speed and angle to the horizon allows you to calculate the entire trajectory;
- the departure angle is equal to the angle of incidence of the body, provided that the initial height is zero;
- vertical movement can be considered independently of horizontal movement;
Note that these properties are valid if the friction force during the flight of the body is negligible. In ballistics, when studying the flight of projectiles, many different factors are taken into account, including friction.
Types of parabolic movement

Depending on the height from which the movement starts, at what height it ends, and how the initial speed is directed, the following types of parabolic movement are distinguished:
- Complete parabola. In this case, the body is thrown from the surface of the earth, and it falls onto this surface, describing a complete parabola.
- Half of a parabola. Such a graph of the motion of the body is observed if it is thrown from a certain height h, directing the velocity v parallel to the horizon, that is, at an angle θ=0o.
- Part of a parabola. Such trajectories arise when a body is thrown at some angle θ≠0o, and the differencethe start and end heights are also non-zero (h-h0≠0). Most object motion trajectories are of this type. For example, a shot from a cannon standing on a hill, or a basketball player throwing a ball into a basket.
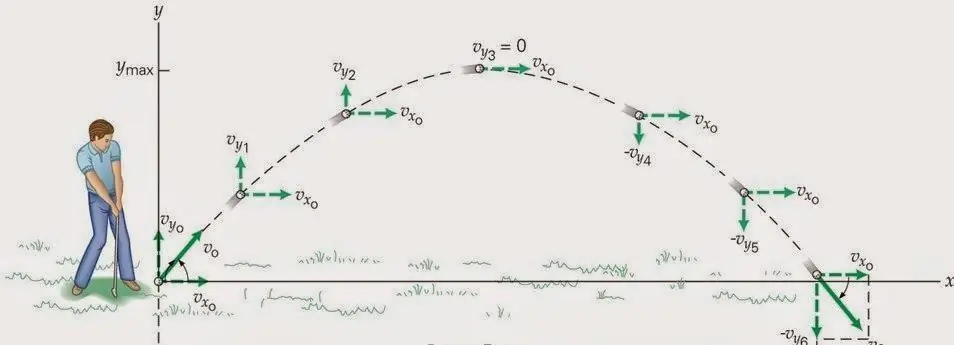
The graph of the movement of the body corresponding to a full parabola is shown above.
Required formulas for calculation
Let's give formulas for describing the motion of a body thrown at an angle to the horizon. Neglecting the force of friction, and taking into account only the force of gravity, we can write two equations for the speed of an object:
vx=v0cos(θ)
vy=v0sin(θ) - gt
Since gravity is directed vertically downwards, it does not change the horizontal component of velocity vx, so there is no time dependence in the first equation. The vy component, in turn, is influenced by gravity, which gives g an acceleration to the body directed towards the ground (hence the minus sign in the formula).
Now let's write formulas for changing the coordinates of a body thrown at an angle to the horizon:
x=x0+v0cos(θ)t
y=y0+ v0sin(θ)t - gt2 /2
Starting coordinate x0often assumed to be zero. The coordinate y0 is nothing but the height h from which the body is thrown (y0=h).
Now let's express the time t from the first expression and substitute it into the second, we get:
y=h + tg(θ)x - g /(2v02cos 2(θ))x2
This expression in geometry corresponds to a parabola whose branches are directed downwards.
The above equations are sufficient to determine any characteristics of this type of movement. So, their solution leads to the fact that the maximum flight range is achieved if θ=45o, while the maximum height to which the thrown body rises is achieved when θ=90 o.






