Tetrahedron in Greek means "tetrahedron". This geometric figure has four faces, four vertices and six edges. The edges are triangles. Basically, a tetrahedron is a triangular pyramid. The first mention of polyhedra appeared long before the existence of Plato.
Today we will talk about the elements and properties of the tetrahedron, and also learn the formulas for finding the area, volume and other parameters of these elements.
Elements of a tetrahedron
The line segment, released from any vertex of the tetrahedron and lowered to the intersection point of the medians of the opposite face, is called the median.
The height of the polygon is a normal segment dropped from the opposite vertex.
A bimedian is a segment connecting the centers of crossing edges.
Properties of a tetrahedron
1) Parallel planes that pass through two skew edges form a circumscribed box.
2) A distinctive property of a tetrahedron is thatthe medians and bimedians of the figure meet at the same point. It is important that the latter divides the medians in a ratio of 3:1, and bimedians - in half.
3) A plane divides a tetrahedron into two parts of equal volume if it passes through the middle of two crossing edges.
Types of tetrahedron
The species diversity of the figure is quite wide. A tetrahedron can be:
- correct, that is, at the base of an equilateral triangle;
- equihedral, in which all faces are the same in length;
- orthocentric when the heights have a common point of intersection;
- rectangular if the flat corners at the top are normal;
- proportionate, all bi heights are equal;
- wireframe if there is a sphere that touches edges;
- incentric, that is, the segments dropped from the vertex to the center of the inscribed circle of the opposite face have a common intersection point; this point is called the centroid of the tetrahedron.
Let's dwell on the regular tetrahedron, the properties of which are practically the same.
Based on the name, you can understand that it is called so because the faces are regular triangles. All the edges of this figure are congruent in length, and the faces are congruent in area. A regular tetrahedron is one of five similar polyhedra.
Tetrahedron formulas
The height of a tetrahedron is equal to the product of the root of 2/3 and the length of the edge.
The volume of a tetrahedron is found in the same way as the volume of a pyramid: the square root of 2 divided by 12 and multiplied by the length of the edge in the cube.
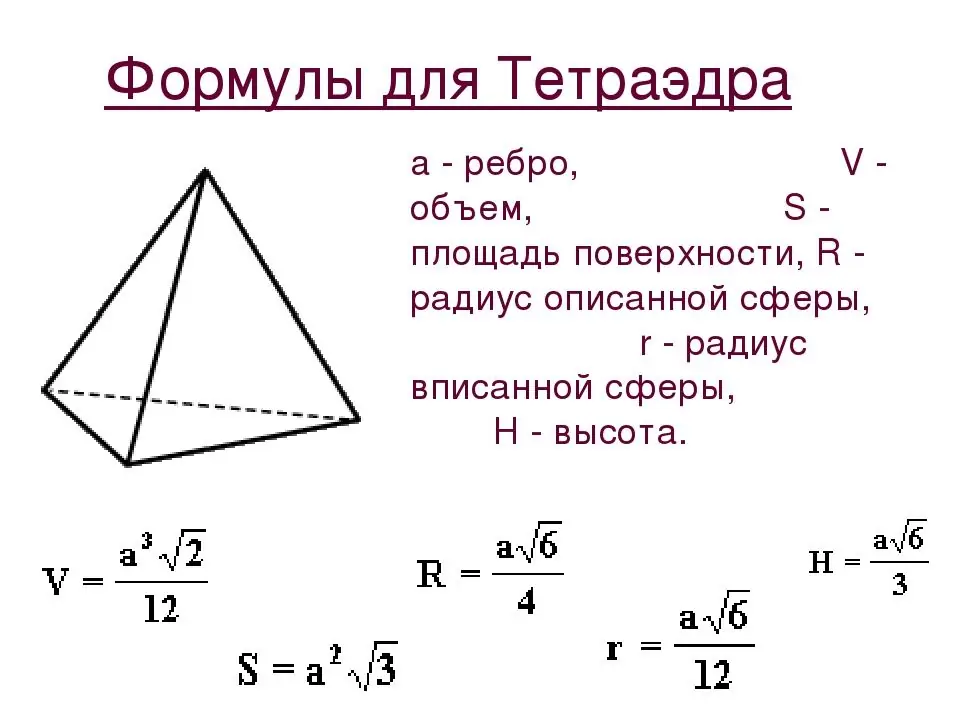
The rest of the formulas for calculating the area and radii of circles are presented above.






