In higher mathematics, such a concept as a transposed matrix is studied. It should be noted that many people think that this is a rather complicated subject that cannot be mastered. However, it is not. In order to understand exactly how such an easy operation is carried out, it is only necessary to familiarize yourself a little with the basic concept - the matrix. The topic can be understood by any student if he takes the time to study it.
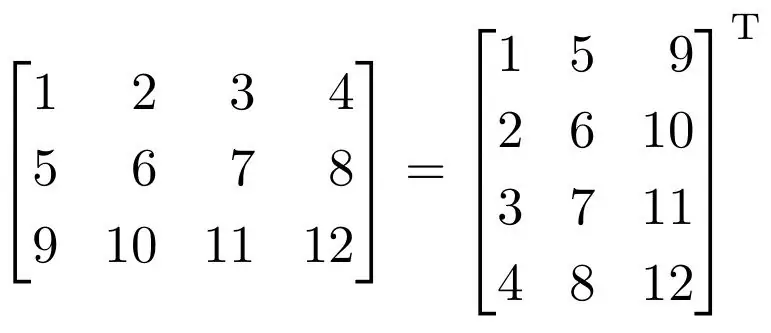
What is a matrix?
Matrices are quite common in mathematics. It should be noted that they also occur in computer science. Thanks to them and with their help, it is easy to program and create software.
What is a matrix? This is the table in which the elements are placed. It has to be rectangular. In simple terms, a matrix is a table of numbers. It is denoted by any capital Latin letters. It can be rectangular or square. There isalso separate rows and columns, which are called vectors. Such matrices receive only one line of numbers. In order to understand what size a table has, you need to pay attention to the number of rows and columns. The first is denoted by the letter m, and the second - n.
It is imperative to understand what the diagonal of a matrix is. There is a side and main. The second is that strip of numbers that goes from left to right from the first to the last element. In this case, the side line will be from right to left.
With matrices, you can do almost all the simplest arithmetic operations, that is, add, subtract, multiply among themselves and separately by a number. They can also be transposed.

Transposition process
A transposed matrix is a matrix in which rows and columns are reversed. This is done as easily as possible. Designated as A with a superscript T (AT). In principle, it should be said that in higher mathematics this is one of the simplest operations on matrices. The table size is preserved. Such a matrix is called transposed.
Properties of transposed matrices
In order to do the transposition process correctly, you need to understand what properties of this operation exist.
- There must be an initial matrix to any transposed table. Their determinants must be equal.
- If there is a scalar unit, then it can be taken out when performing this operation.
- When the matrix is transposed twice, it willequal to the original.
- If we compare two stacked tables with columns and rows changed, with the sum of the elements on which this operation was performed, they will be the same.
- The last property is that if you transpose tables multiplied with each other, then the value should be equal to the results obtained in the course of multiplying the transposed matrices in reverse order.
Why transpose?
A matrix in mathematics is necessary in order to solve certain problems with it. Some of them require the inverse table to be computed. To do this, you need to find a determinant. Next, the elements of the future matrix are calculated, then they are transposed. It remains to find only the directly inverse table. We can say that in such problems it is required to find X, and this is quite easy to do with the help of basic knowledge of the theory of equations.

Results
In this article, it was considered what a transposed matrix is. This topic will be useful for future engineers who need to be able to correctly calculate complex structures. Sometimes the matrix is not so easy to solve, you have to break your head. However, in the course of student mathematics, this operation is carried out as easily and without any effort.






