Pythagoras argued that the number underlies the world along with the basic elements. Plato believed that the number connects the phenomenon and the noumenon, helping to cognize, measure and draw conclusions. Arithmetic comes from the word "arithmos" - a number, the beginning of beginnings in mathematics. It can describe any object - from an elementary apple to abstract spaces.
Needs as a development factor
In the early stages of the formation of society, people's needs were limited to the need to keep count - one sack of grain, two sacks of grain, etc. Natural numbers were enough for this, the set of which is an infinite positive sequence of integers N.
Later, with the development of mathematics as a science, there was a need for a separate field of integers Z - it includes negative values and zero. Its appearance at the household level was provoked by the fact that in the primary accounting it was necessary to somehow fixdebts and losses. On a scientific level, negative numbers have made it possible to solve the simplest linear equations. Among other things, the image of a trivial coordinate system has now become possible, since a reference point has appeared.
The next step was the need to introduce fractional numbers, since science did not stand still, more and more discoveries required a theoretical basis for a new growth impetus. This is how the field of rational numbers appeared Q.

Finally, rationality ceased to satisfy requests, because all new conclusions required justification. There appeared the field of real numbers R, the works of Euclid on the incommensurability of certain quantities due to their irrationality. That is, ancient Greek mathematicians positioned the number not only as a constant, but also as an abstract quantity, which is characterized by the ratio of incommensurable quantities. Due to the fact that real numbers appeared, such quantities as "pi" and "e" "saw the light", without which modern mathematics could not take place.
The final innovation was the complex number C. It answered a number of questions and refuted the previously introduced postulates. Due to the rapid development of algebra, the outcome was predictable - having real numbers, solving many problems was impossible. For example, thanks to complex numbers, the theory of strings and chaos stood out, and the equations of hydrodynamics expanded.

Set theory. Cantor
The concept of infinity at all timescaused controversy, since it could neither be proved nor disproved. In the context of mathematics, which operated with strictly verified postulates, this manifested itself most clearly, especially since the theological aspect still had weight in science.
However, thanks to the work of the mathematician Georg Kantor, everything fell into place over time. He proved that there are an infinite number of infinite sets, and that the field R is greater than the field N, even if they both have no end. In the middle of the 19th century, his ideas were loudly called nonsense and a crime against classical, unshakable canons, but time put everything in its place.
Basic properties of the field R
Real numbers not only have the same properties as the subsets that are included in them, but are also supplemented by others due to the scale of their elements:
- Zero exists and belongs to the field R. c + 0=c for any c from R.
- Zero exists and belongs to the field R. c x 0=0 for any c from R.
- The relation c: d for d ≠ 0 exists and is valid for any c, d from R.
- The field R is ordered, that is, if c ≦ d, d ≦ c, then c=d for any c, d from R.
- Addition in the field R is commutative, i.e. c + d=d + c for any c, d from R.
- Multiplication in the field R is commutative, i.e. c x d=d x c for any c, d from R.
- Addition in the field R is associative, i.e. (c + d) + f=c + (d + f) for any c, d, f from R.
- Multiplication in the field R is associative, i.e. (c x d) x f=c x (d x f) for any c, d, f from R.
- For every number in the field R, there is an opposite, such that c + (-c)=0, where c, -c is from R.
- For each number from the field R, its inverse exists, such that c x c-1 =1, where c, c-1 from R.
- The unit exists and belongs to R, so c x 1=c, for any c from R.
- The distribution law is valid, so c x (d + f)=c x d + c x f, for any c, d, f from R.
- In field R, zero is not equal to one.
- The field R is transitive: if c ≦ d, d ≦ f, then c ≦ f for any c, d, f from R.
- In the field R, order and addition are related: if c ≦ d, then c + f ≦ d + f for any c, d, f from R.
- In the field R, order and multiplication are related: if 0 ≦ c, 0 ≦ d, then 0 ≦ c x d for any c, d from R.
- Both negative and positive real numbers are continuous, that is, for any c, d from R, there is an f from R such that c ≦ f ≦ d.
Module in field R
Real numbers include modulus.
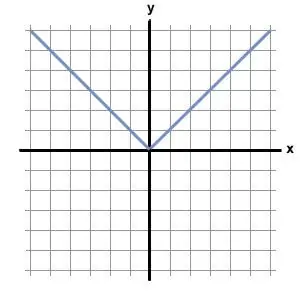
Denoted as |f| for any f from R. |f|=f if 0 ≦ f and |f|=-f if 0 > f. If we consider the modulus as a geometric quantity, then it is the distance traveled - it doesn’t matter if you “passed” zero to minus or forward to plus.
Complex and real numbers. What are the similarities and what are the differences?
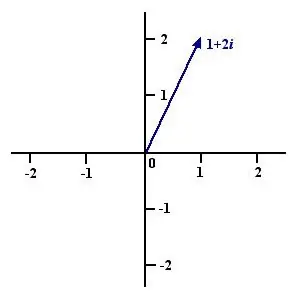
By and large, complex and real numbers are one and the same, except that the first has joinedimaginary unit i, whose square is -1. The elements of the fields R and C can be represented as the following formula:
c=d + f x i, where d, f belong to the field R and i is the imaginary unit
To get c from R in this case, f is simply taken equal to zero, that is, only the real part of the number remains. Due to the fact that the field of complex numbers has the same set of properties as the field of real numbers, f x i=0 if f=0.
Regarding practical differences, for example, in the R field, the quadratic equation is not solved if the discriminant is negative, while the C field does not impose such a restriction due to the introduction of the imaginary unit i.
Results
The "bricks" of the axioms and postulates on which mathematics is based do not change. Due to the increase in information and the introduction of new theories, the following "bricks" are placed on some of them, which in the future can become the basis for the next step. For example, natural numbers, despite the fact that they are a subset of the real field R, do not lose their relevance. It is on them that all elementary arithmetic is based, with which human knowledge of the world begins.
From a practical point of view, real numbers look like a straight line. On it you can choose the direction, designate the origin and step. A straight line consists of an infinite number of points, each of which corresponds to a single real number, regardless of whether it is rational or not. It is clear from the description that we are talking about a concept on which both mathematics in general and mathematical analysis in general are built.particular.






