Among the main characteristics of maps of the area, this one is most often singled out. This is scale accuracy. In the article we will analyze what this concept hides in itself. We will also consider what scale is in general, we will characterize its main varieties. Let's analyze how the concept of "graphical accuracy" is related to the subject of our conversation.
What is this?
Scale is an important clarification showing how much each line that was drawn on the drawing, plan, is less or more than the real size of the object it depicts. Such clarifications are presented on drawing documents and maps both numerically and graphically.
Scale of plans, accuracy of scale - concepts that can be found in a wide variety of areas:
- Cartography.
- Design.
- Geodesy.
- Photo.
- Modeling.
- Programming.
- Math.
- Cinema.
Some of these applications, their features, we will consider in the course of the article.
Scaling accuracy
And nowdefinition of the key concept. Scale accuracy - part of the horizontal line spacing, which will mean 0.1 mm on the drawing. Why was this value chosen?
0, 1 mm is accepted here due to the fact that this is the smallest segment that can be distinguished by the human eye in the image without the use of special equipment, tools, devices.
Let's take a concrete example. Given 1:10000. The accuracy of the scale will be, respectively, 1 m. Let's analyze in more detail:
- 1 cm on a plan or image is 10,000 cm (or 100 m) on the real terrain.
- 1 mm in the image is 1,000 cm (or 10 m).
- 0, 1mm is 100cm (or 1m) on real terrain.
Thus, it is easy to determine the maximum accuracy of the scale. This is the distance of the real surface, equal to 0.1 mm on the map - the minimum segment that a person can distinguish.
Graphic fidelity
And now let's get acquainted with the graphic accuracy of scales. This is another significant feature when using plans and maps.
Graphic accuracy is associated with the resolution "and" of the human eye. In turn, it makes "G". Hence G=u.
That is, if the angle "and" between the vectors into two points "B" and "L" when viewed by an observer with a normal level of vision is "G" or more, then they will be perceived as two points. If this angle to the concept of resolution is less than "G", then "L" and "B" will be perceived by a person as onedot.
It is best to get acquainted with the definition of scale accuracy on a specific example. Let's say a person examines the map from the best distance "b", equal to 35 cm. The value of G=u. Now you need to determine the smallest distance (that is, graphical accuracy) between "B" and "L", at which they will still be perceived by the observer as two different points. Here is the calculation:
1 - is! - 1/3438 x 350 mm=0.1 mm.
1/3438 is the value of the angle u=r, which in this case is expressed in radians (3438' is the number of minutes in a radian).
Thus, the output value of 0.1 mm is the graphic accuracy of the plan or map.
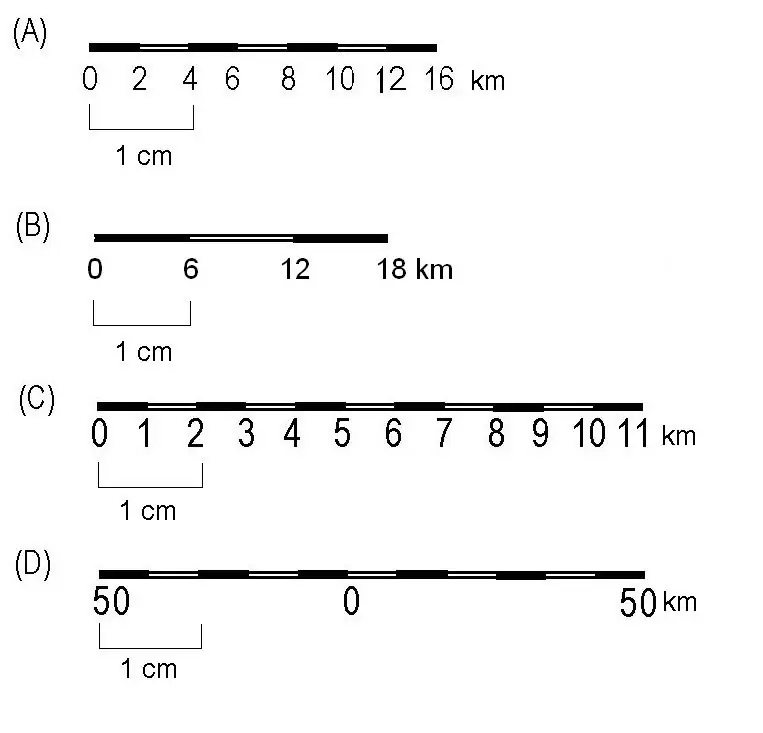
Connection of concepts
Now let's see how the above term relates to the main one. Scale accuracy is, as we remember, the distance on the surface of the Earth, which is equal to 0.1 mm on the document.
You can derive the formula:
T=gM=0.1 M mm.
Decipher its elements:
- T - scale accuracy.
- M is the scale denominator.
- r=0.1 mm - graphic accuracy.
From here we can deduce the related interpretation. Scale accuracy - graphical accuracy, which is expressed in the scale of a map or plan. And what is the result? Graphic accuracy will become a constant (0.1 mm) for all existing scales.
Accordingly, the scale accuracy will change along with it. It will be the higher, the larger the compiler chose the scale.
And nowwe will deal with the features of such a characteristic as scale in various fields of application.

Design, geodesy and cartography
We know what "500" scale accuracy means - 1:500. Let us now consider what varieties of it are typical for the field of design, cartography and geodesy:
- Numerical scale. The indicator is written as a fraction. Its numerator will be one, and its denominator will be some degree of projection reduction on the map. For example, let's take a scale of 1:5,000. It means that 1 cm on a plan, map is 5,000 cm (or 50 m) on a real terrain. Accordingly, there will be a larger scale that has a smaller denominator. So, 1:1,000 will be larger than 1:20,000.
- Named scale. The compiler of the map prescribes on the document what distance on the real terrain is equal to 1 cm on the plan. Here is an example: "There are 1000 kilometers in 1 centimeter". Or in short: "1 cm=100 km".
- Graphic scale. In turn, it will be divided into transverse and linear. We will analyze them separately.

Varieties of graphic category
What is the accuracy of the scale - the transverse scale? Let's get acquainted with the characteristics:
- Linear. Such a graphical scale on the map is represented as a ruler, which will be divided into real parts.
- Transverse. This is a graphic scale represented as a nomogram. Its construction is based on the proportionality of the parts of parallel lines that intersect the sides of the angle. This scale is applicable for a more accurate measurement of the length of lines on the plans. They use it in this way: they measure the length on the bottom line of a given transverse scale so that the right end is at a whole distance (OM), and the left one is beyond 0. If in this case the left leg is between tenth divisions, respectively, of the left segment (from 0), then the specialist raises both legs of the meter up. Until the left leg of the meter is already at the intersection of any horizontal line and any transversal. But the right leg should also be on this horizontal line. The minimum CD here is 0.2 mm. Accordingly, the smallest accuracy is 0.1 mm.
Series of image scales in design
We already know what 1:500 scale precision means. But in what cases does the compiler choose it? Let's analyze this question:
- Scaling down. Accordingly, they are used in cases where it is necessary to depict an object on a plan, a terrain that significantly exceeds its area. If the compiler turns to the design of master plans of especially large sizes, then he will need to use the following scales: 1:2,000, 1:5,000, 1:10,000, 1:20,000, 1:25,000, 1:50,000.
- Actual size. If you want to depict the object on the plan "as it is", then refer to the scale "one to one". Accordingly, 1 cm of real length here will correspond to 1 cm of length on the plan.
- Scalesmagnification. Necessary in cases when it is required to depict an object that is too small on the plan for a detailed acquaintance with its appearance, device.
In photo
Of course, 1:10,000 scale accuracy is more associated with cartography. But this applies to the world of photography as well. The scale here means the ratio of the so-called linear dimensions of the image obtained on an ultrasensitive matrix or on photographic film to the size of the projection of the corresponding projection zone on a plane that is perpendicular to the camera.
There are photographers who measure the scale as the ratio of the size of a real object to its size on a screen, photographic paper or other media. But the correct way to determine the scale in a photograph depends only on the context in which the image is used.
In photography, the scale is also important when calculating the depth of any sharply depicted object, space. Today, specialists have access to a very wide range of scales from infinitely small (used when shooting distant celestial bodies) to very large (without the use of special optical attachments, for example, today it is possible to get a 10:1 scale image).
Here, macro photography is already considered to be shooting at a scale of 1: 1 (and, accordingly, larger). But with the spread of digital compact cameras, macro photography has also come to be called the style when the lens is placed too close to the subject. Considering the classical definition, thensuch an interpretation would not be correct.

In modeling
For each type of bench (or scale) modeling, its own scales are defined. They consist of several scales characterized by a certain degree of reduction. Interestingly, for each type of modeling (railway, automobile, ship modeling, military equipment, aircraft modeling) there are certain historically formed scale series that do not intersect with others.
Here the scale is calculated by a simple formula:
L / M=X.
Decipher:
- L - original parameters.
- M - scale required for work.
- X is the desired value.
In programming
In this area, the so-called time scale will be important. Let's find out what it is.
In a time-sharing OS, it is very important to provide "real-time" to specific tasks. It differs in that the processing of external events goes without additional delays or gaps. Here one more concept will be important - "real time scale". But it should be understood that it has no direct relation to the scale on the maps. This is just a terminological convention.
In film technology
In film technology, the accuracy of the time scale is also important. The latter means a quantitative indicator of slowing down or accelerating the movement, which will be equal to the ratio of the projection frame rate to the shooting rate.
Consider this in simple termsexample. The projection frame rate for film shooting is 24 fps. Filming was carried out at the same time "at a speed" of 72 frames / sec. The time scale in this case will be 1:3.
And what will mean, for example, 2:1? This is twice as fast as the standard flow of what is happening on the screen.
In mathematics
In this area, scale refers to the linear relationship of two dimensions. Also, in many practically applicable areas, this will be the ratio of the image size to the actual size of the image.
In mathematics, the scale is the ratio of any distance on the map to the real distance on the real terrain. If we look at the example, this is the same as in cartography. Let's say 1:100,000,000. So, 1 cm in the image is 100,000 cm in reality. That is, a thousand meters or one kilometer.
Scale is a widely applicable characteristic. This is a standard and integral component in the development of plans, drawings of objects, maps of the area. It is used in designing, in geodesy, cartography, relevant in photography, film technology, programming and mathematics. It itself is mainly characterized by accuracy - the ratio of the real distance to the accepted one on the map.






