Students of higher mathematics should be aware that the sum of some power series belonging to the interval of convergence of the given series turns out to be a continuous and unlimited number of times differentiated function. The question arises: is it possible to assert that a given arbitrary function f(x) is the sum of some power series? That is, under what conditions can the function f(x) be represented by a power series? The importance of this question lies in the fact that it is possible to approximately replace the function f(x) by the sum of the first few terms of the power series, that is, by a polynomial. Such a replacement of a function by a rather simple expression - a polynomial - is also convenient when solving some problems of mathematical analysis, namely: when solving integrals, when calculating differential equations, etc.
It has been proved that for some function f(х) where derivatives up to (n+1)th order, including the last one, can be calculated in the neighborhood (α - R; x0 + R) of some point x=α the formula is valid:
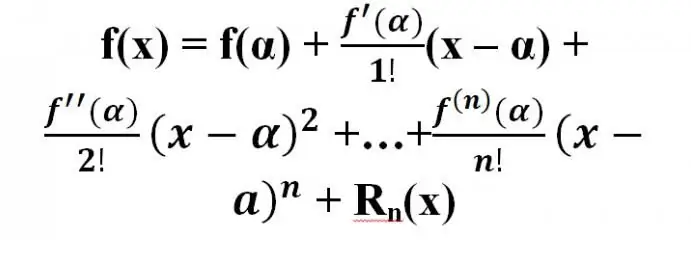
This formula is named after the famous scientist Brook Taylor. The series that is obtained from the previous one is called the Maclaurin series:
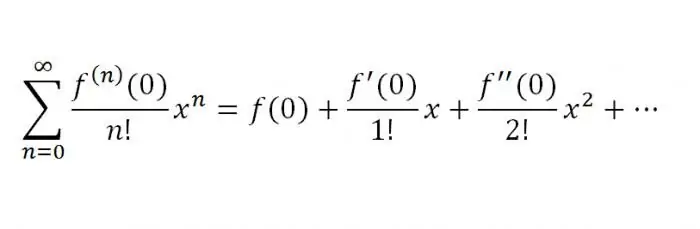
The rule that makes it possible to expand in a Maclaurin series:
- Determine derivatives of the first, second, third… orders.
- Calculate what the derivatives at x=0 are equal to.
- Record the Maclaurin series for this function, and then determine the interval of its convergence.
- Determine the interval (-R;R) where the remainder of the Maclaurin formula
R (x) -> 0 for n -> infinity. If one exists, the function f(x) in it must coincide with the sum of the Maclaurin series.
Now consider the Maclaurin series for individual functions.
1. So, the first one will be f(x)=ex. Of course, according to its features, such a function has derivatives of various orders, and f(k)(x)=ex, where k equals all natural numbers. Let's substitute x=0. We get f(k)(0)=e0=1, k=1, 2… would look like this:
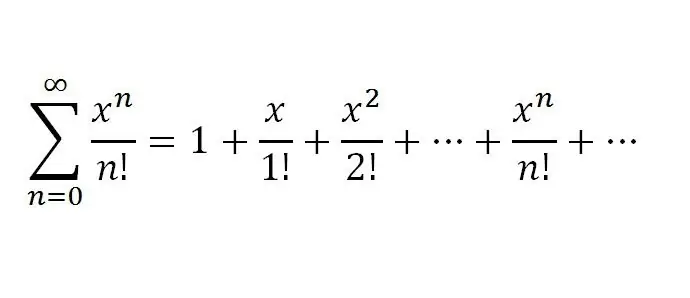
2. The Maclaurin series for the function f(x)=sin x. Immediately clarify that the function for all unknowns will have derivatives, besides f'(x)=cos x=sin(x+n/2), f ''(x)=-sin x=sin(x+2n/2)…, f(k)(x)=sin(x+k n/2), where k is equal to any natural number. That is, after making simple calculations, we can come to the conclusion that the series for f(x)=sin x will look like this:
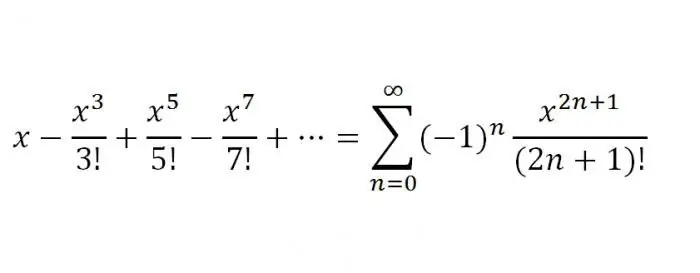
3. Now let's try to consider the function f(x)=cos x. She's for all the unknownhas derivatives of arbitrary order, and |f(k)(x)|=|cos(x+kp/2)|<=1, k=1, 2… Again, after doing some calculations, we get that the series for f(x)=cos x will look like this:
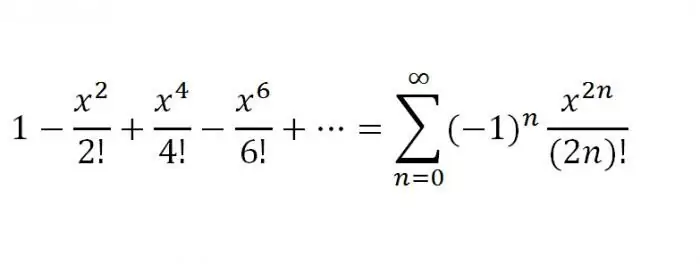
So, we have listed the most important functions that can be expanded in the Maclaurin series, but they are supplemented by Taylor series for some functions. Now we will list them. It is also worth noting that Taylor and Maclaurin series are an important part of the practice of solving series in higher mathematics. So, Taylor series.
1. The first will be a series for f-ii f(x)=ln(1+x). As in the previous examples, given us f (x)=ln (1 + x), we can add a series using the general form of the Maclaurin series. however, for this function, the Maclaurin series can be obtained much more simply. After integrating a certain geometric series, we get a series for f(x)=ln(1+x) of this sample:
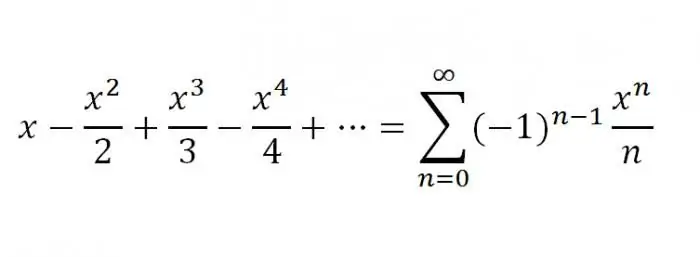
2. And the second, which will be final in our article, will be a series for f (x) u003d arctg x. For x belonging to the interval [-1;1], the expansion is valid:
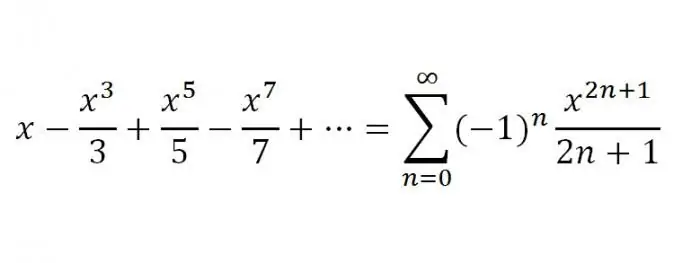
That's it. This article examined the most commonly used Taylor and Maclaurin series in higher mathematics, in particular, in economic and technical universities.






