Triangle is the simplest figure closed on the plane, consisting of only three interconnected segments. In geometry problems, it is often necessary to determine the area of \u200b\u200bthis figure. What do you need to know for this? In the article we will answer the question of how to find the area of a triangle on three sides.
General formula
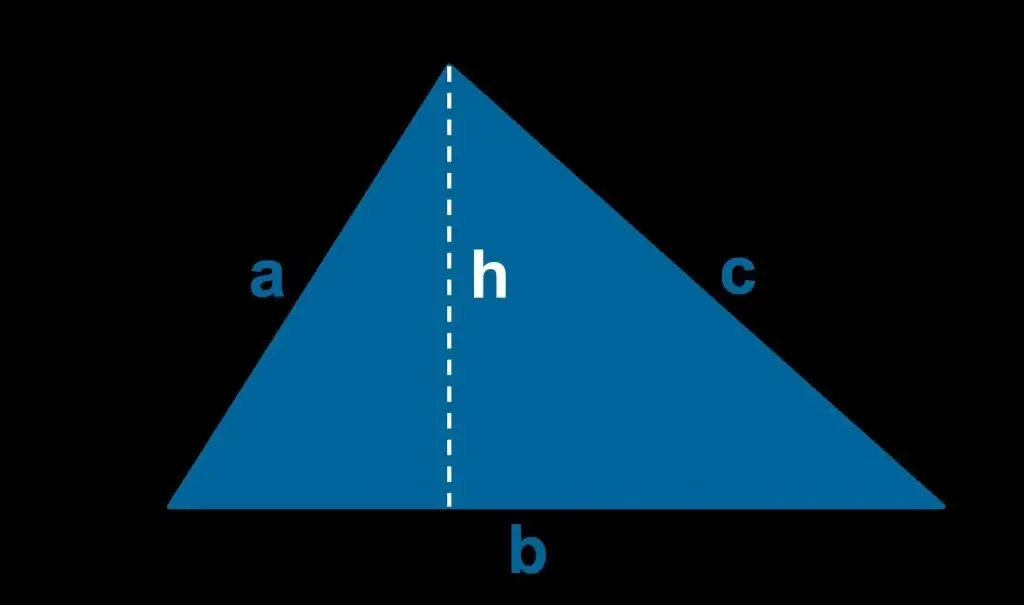
Every student knows that the area of a triangle is calculated as the product of the length of any of its sides - a by half the height - h, lowered to the chosen side. Below is the corresponding formula: S=ah/2.
This expression can be used if at least two sides and the value of the angle between them are known. In this case, the height h is easy to calculate using trigonometric functions, such as the sine. But not everyone knows how to find the area on three sides of a triangle.
Heron's Formula
This formula is the answer to the question of howthree sides find the area of the triangle. Before writing it down, let's denote the lengths of the segments of an arbitrary figure as a, b and c. Heron's formula is written as follows: S=√(p(p-a)(p-b)(p-c)).
Where p is the half-perimeter of the figure, i.e.: p=(a+b+c)/2.
Despite the apparent cumbersomeness, the above expression for the area S is easy to remember. To do this, you must first calculate the semi-perimeter of the triangle, then subtract from it by one length of the side of the figure, multiply all the differences obtained and the semi-perimeter itself. Finally, take the square root of the product.

This formula is named after Heron of Alexandria, who lived at the beginning of our era. Modern history believes that it was this philosopher who first applied this expression to perform the corresponding calculations. This formula is published in his Metrica, which dates back to 60 AD. Note that some of the works of Archimedes, who lived two centuries earlier than Heron, contain signs that the Greek philosopher already knew the formula. In addition, the ancient Chinese also knew how to find the area of a triangle, knowing three sides.
It is important to note that the problem can be solved without knowing the existence of Heron's formula. To do this, draw a couple of heights in the triangle and use the general formula from the previous paragraph, compiling the appropriate system of equations.
Heron's expression can be used to calculate the areas of arbitrary polygons, after splitting them intotriangles and calculating the lengths of the resulting diagonals.
Example of problem solving
Knowing how to find the area of a triangle on three sides, we will consolidate our knowledge by solving the following problem. Let the sides of the figure be 5 cm, 4 cm and 3 cm. Find the area.
Three sides of a triangle are known, so you can use Heron's formula. We calculate the semi-perimeter and the necessary differences, we have:
- p=(a+b+c)/2=6 cm;
- p-a=1cm;
- p-b=2cm;
- p-c=3 cm.
Then we get the area: S=√(p(p-a)(p-b)(p-c))=√(6123)=6 cm2.
The triangle given in the condition of the problem is right-angled, which is easy to check if you use the Pythagorean theorem. Since the area of such a triangle is half the product of the legs, we get: S=43/2=6 cm2.
The resulting value is the same as for Heron's formula, which confirms the validity of the latter.






