Surface area of a straight prism: formulas and an example of a problem

2024 Author: Angel Austin | [email protected]. Last modified: 2024-01-02 17:39

Volume and surface area are two important characteristics of any body that has finite dimensions in three-dimensional space. In this article, we consider a well-known class of polyhedra - prisms. In particular, the question of how to find the surface area of a straight prism will be revealed.

What is a prism?

A prism is any polyhedron that is bounded by several parallelograms and two identical polygons located in parallel planes. These polygons are considered the bases of the figure, and its parallelograms are the sides. The number of sides (corners) of the base determines the name of the figure. For example, the figure below shows a pentagonal prism.

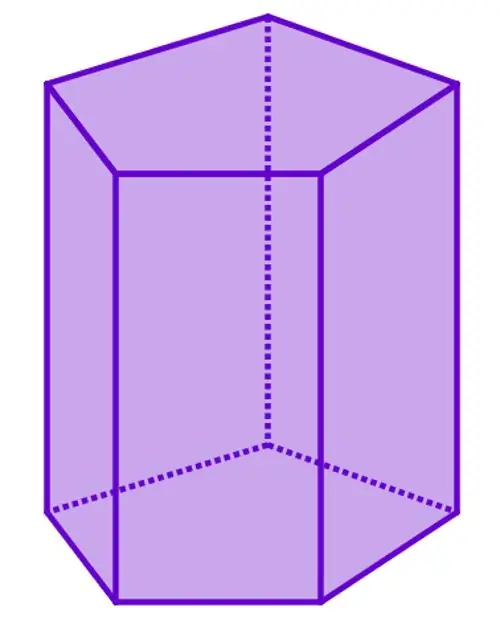
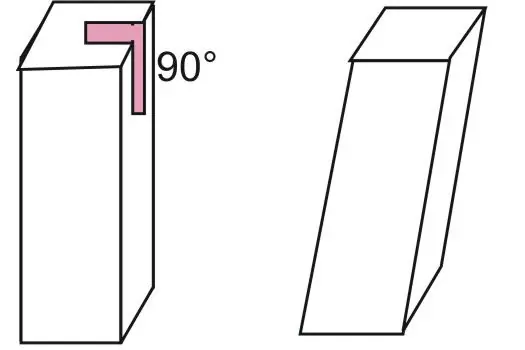
The distance between the bases is called the height of the figure. If the height is equal to the length of any side edge, then such a prism will be straight. The second sufficient feature for a straight prism is that all its sides are rectangles or squares. If, thoughIf one side is a general parallelogram, then the figure will be inclined. Below you can see how the straight and oblique prisms visually differ on the example of quadrangular figures.

Surface area of a straight prism

If a geometric figure has an n-gonal base, then it consists of n+2 faces, n of which are rectangles. Let's denote the lengths of the sides of the base as a_i, where i=1, 2, …, n, and denote the height of the figure, which is equal to the length of the side edge, as h. To determine the area (S) of the surface of all faces, add the area S_{o of each of the bases and all the areas of the sides (rectangles). Thus, the formula for S in general form can be written as follows:}

S=2S_o+ S_b

Where S_{b is the lateral surface area.}

Since the base of a straight prism can be absolutely any flat polygon, then a single formula for calculating S_{ocannot be given, and to determine this value, in the general case, geometric analysis should be carried out. For example, if the base is a regular n-gon with side a, then its area is calculated by the formula:}

S_o=n/4ctg(pi/n)a²

As for the value of S_{b, the expression for its calculation can be given. The lateral surface area of a straight prism is:}

S_b=h∑_i=1(a_i)

That is, the valueS_{b is calculated as the product of the figure's height and the perimeter of its base.}

Example of problem solving

Let's apply the acquired knowledge to solve the following geometric problem. Given a prism, the base of which is a right triangle with sides at a right angle of 5 cm and 7 cm. The height of the figure is 10 cm. It is necessary to find the surface area of a right triangular prism.

First, let's calculate the hypotenuse of the triangle. It will be equal to:

c=√(5²+ 7^{2)=8.6 cm}

Now let's do one more preparatory mathematical operation - calculate the perimeter of the base. It will be:

P=5 + 7 + 8.6=20.6cm

The area of the lateral surface of the figure is calculated as the product of the value P and the height h=10 cm, that is, S_b=206 cm^2.

To find the area of the entire surface, two base areas should be added to the found value. Since the area of a right triangle is determined by half the product of the legs, we get:

2S_o=257/2=35cm²

Then we get that the surface area of a straight triangular prism is 35 + 206=241 cm2.