One of the important questions in the study of thermodynamic systems in physics is the question of whether this system can perform some useful work. Closely related to the concept of work is the concept of internal energy. In this article, we will consider what the internal energy of an ideal gas is and give formulas for calculating it.
Ideal gas
About gas, as a state of aggregation, which does not have any elastic force under external influence on it and, as a result, does not retain volume and shape, every schoolchild knows. The concept of an ideal gas for many remains incomprehensible and unclear. Let's explain it.
An ideal gas is any gas that satisfies the following two important conditions:
- The particles that make it up have no size. They do have a size, but it is so small compared to the distances between them that it can be ignored in all mathematical calculations.
- Particles do not interact with each other using van der Waals forces or forcesother nature. In fact, in all real gases, such an interaction is present, but its energy is negligible compared to the average energy of the kinetic particles.
The described conditions are satisfied by almost all real gases, the temperatures of which are above 300 K, and the pressures do not exceed one atmosphere. For too high pressures and low temperatures observes the deviation of gases from the ideal behavior. In this case, one speaks of real gases. They are described by the van der Waals equation.
The concept of the internal energy of an ideal gas
In accordance with the definition, the internal energy of a system is the sum of the kinetic and potential energies contained within this system. If this concept is applied to an ideal gas, then the potential component should be discarded. Indeed, since the particles of an ideal gas do not interact with each other, they can be considered as moving freely in absolute vacuum. To extract one particle from the system under study, it is not necessary to do work against the internal forces of interaction, since these forces do not exist.
Thus, the internal energy of an ideal gas always coincides with its kinetic energy. The latter, in turn, is uniquely determined by the molar mass of the particles of the system, their number, as well as the average speed of translational and rotational motion. The speed of movement depends on the temperature. An increase in temperature leads to an increase in internal energy, and vice versa.
Formula forinternal energy
Denote the internal energy of an ideal gas system with the letter U. According to thermodynamics, it is defined as the difference between the enthalpy H of the system and the product of pressure and volume, that is:
U=H - pV.
In the paragraph above, we found out that the value of U corresponds to the total kinetic energy Ekof all gas particles:
U=Ek.
From statistical mechanics, within the framework of the molecular kinetic theory (MKT) of an ideal gas, it follows that the average kinetic energy of one particle Ek1 is equal to the following value:
Ek1=z/2kBT.
Here kB and T - Boltzmann constant and temperature, z - number of degrees of freedom. The total kinetic energy of the system Ek can be obtained by multiplying Ek1 by the number of particles N in the system:
Ek=NEk1=z/2NkBT.
Thus, we have obtained the formula for the internal energy of an ideal gas, written in general form in terms of the absolute temperature and the number of particles in a closed system:
U=z/2NkBT.
Monatomic and polyatomic gas
The formula for U written in the previous paragraph of the article is inconvenient for its practical use, since it is difficult to determine the number of particles N. However, if we take into account the definition of the amount of substance n, then this expression can be rewritten in a more convenient form:
n=N/NA; R=NAkB=8, 314 J/(molK);
U=z/2nR T.
The number of degrees of freedom z depends on the geometry of the particles that make up the gas. Thus, for a monoatomic gas, z=3, since an atom can move independently only in three directions of space. If the gas is diatomic, then z=5, since two more rotational degrees of freedom are added to the three translational degrees of freedom. Finally, for any other polyatomic gas, z=6 (3 translational and 3 rotational degrees of freedom). With this in mind, we can write in the following form the formulas for the internal energy of an ideal gas of monatomic, diatomic and polyatomic:
U1=3/2nRT;
U2=5/2nRT;
U≧3=3nRT.
Example of a task to determine internal energy
A 100-liter cylinder contains pure hydrogen at a pressure of 3 atmospheres. Assuming hydrogen to be an ideal gas under given conditions, it is necessary to determine what its internal energy is.

The above formulas for U contain the amount of substance and the temperature of the gas. In the condition of the problem, absolutely nothing is said about these quantities. To solve the problem, it is necessary to recall the universal Clapeyron-Mendeleev equation. It has the appearance shown in the figure.
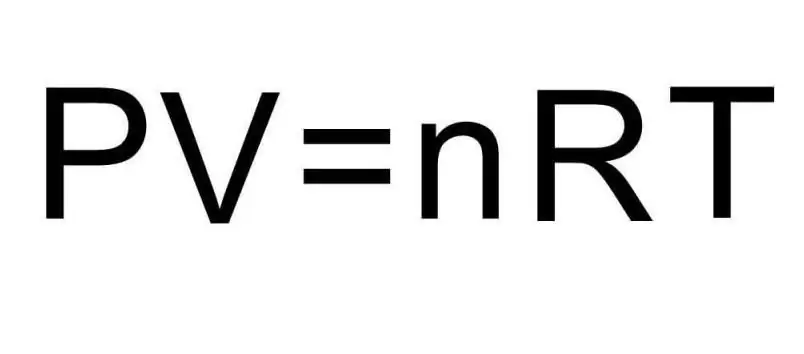
Since hydrogen H2 is a diatomic molecule, the formula for internal energy is:
UH2=5/2nRT.
Comparing both expressions, we arrive at the final formula for solving the problem:
UH2=5/2PV.
It remains to convert the units of pressure and volume from the condition to the SI system of units, substitute the corresponding values in the formula for UH2and get the answer: UH2 ≈ 76 kJ.






