As you know, any physical quantity belongs to one of two types, it is either scalar or vector. In this article, we will consider such kinematic characteristics as speed and acceleration, and also show where the acceleration and speed vectors are directed.
What is speed and acceleration?
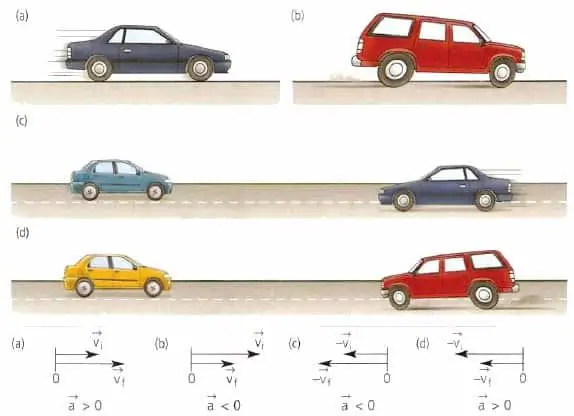
Both of the quantities mentioned in this paragraph are important characteristics of any kind of movement, whether it is moving a body in a straight line or along a curved path.
Speed is the rate at which coordinates change over time. Mathematically, this value is equal to the time derivative of the distance traveled, that is:
v¯=dl¯/dt.
Here the vector l¯ is directed from the start point of the path to the end point.
In turn, acceleration is the speed with which the speed itself changes in time. In the form of a formula, it can be written like this:
a¯=dv¯/dt.
Obviously, taking the second derivative ofdisplacement vector l¯ in time, we will also get the value of the acceleration.
Since speed is measured in meters per second, acceleration, according to the written expression, is measured in meters per second squared.

Where are the acceleration and velocity vectors?
In physics, any mechanical motion of a body is usually characterized by a certain trajectory. The latter is some imaginary curve along which the body moves in space. For example, a straight line or a circle are prime examples of common motion paths.
The body's velocity vector is always directed in the direction of movement, regardless of whether the body slows down or accelerates, whether it moves in a straight line or along a curve. Speaking in geometric terms, the velocity vector is directed tangentially to the point of the trajectory in which the body is currently located.
The acceleration vector of a material or body point has nothing to do with speed. This vector is directed in the direction of speed change. For example, for rectilinear motion, the value a¯ can either coincide in direction with v¯ or be opposite to v¯.
Force acting on the body and acceleration
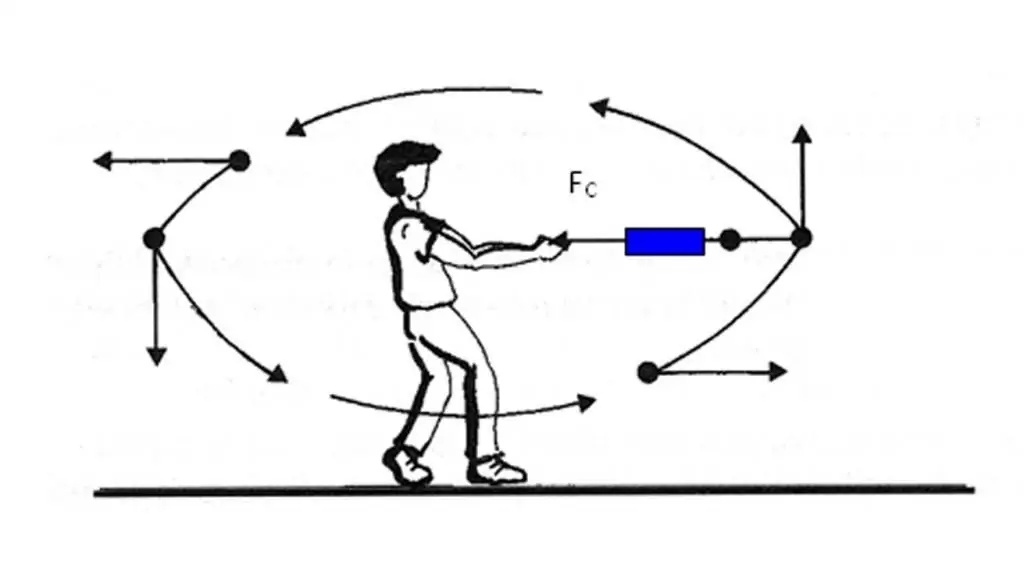
We have found out that the acceleration vector of the body is directed towards the change of the velocity vector. However, it is not always easy to determine how the speed changes at a given point in the trajectory. Moreover, to determine the change in speed, it is necessary to perform the operationvector differences. To avoid these difficulties in determining the direction of the vector a¯, there is another way to quickly find out.
Below is Newton's famous and well-known law to every student:
F¯=ma¯.
The formula shows that the cause of acceleration in bodies is the force acting on them. Since the mass m is a scalar, the force vector F¯ and the acceleration vector a¯ are in the same direction. This fact should be remembered and applied in practice whenever there is a need to determine the direction of the quantity a¯.
If several different forces act on the body, then the direction of the acceleration vector will be equal to the resulting vector of all forces.
Circular motion and acceleration

When a body moves in a straight line, the acceleration is directed either forward or backward. In the case of motion in a circle, the situation is complicated by the fact that the velocity vector is constantly changing its direction. In view of the above, the total acceleration is determined by its two components: tangential and normal accelerations.
Tangential acceleration is directed exactly the same as the velocity vector, or against it. In other words, this acceleration component is directed along the tangent to the trajectory. Tangential acceleration describes the change in the modulus of the speed itself.
Normal acceleration is directed along the normal to the given point of the trajectory, taking into account its curvature. In the case of circular motion, the vector of this component indicatesto the center, that is, the normal acceleration is directed along the radius of rotation. This component is often called centripetal.
Full acceleration is the sum of these components, so its vector can be directed arbitrarily with respect to the circle line.
If the body rotates without changing the linear velocity, then there is only a non-zero normal component, so the full acceleration vector is directed towards the center of the circle. Note that this center is also affected by a force that keeps the body on its trajectory. For example, the gravitational force of the Sun keeps our Earth and other planets in their orbits.






