Prism is a fairly simple geometric three-dimensional figure. Nevertheless, some schoolchildren have problems in determining its main properties, the cause of which, as a rule, is associated with incorrectly used terminology. In this article, we will consider what prisms are, what they are called, and also describe in detail the correct quadrangular prism.
Prism in geometry
The study of three-dimensional figures is a task of stereometry - an important part of spatial geometry. In stereometry, a prism is understood as such a figure, which is formed by the parallel translation of an arbitrary flat polygon at a certain distance in space. Parallel translation implies a movement in which rotation around an axis perpendicular to the plane of the polygon is completely excluded.
As a result of the described method of obtaining a prism, a figure is formed, limited by twopolygons having the same dimensions, lying in parallel planes, and a certain number of parallelograms. Their number coincides with the number of sides (vertices) of the polygon. Identical polygons are called the bases of the prism, and their surface area is the area of the bases. Parallelograms connecting two bases form a side surface.
Prism elements and Euler's theorem
Since the three-dimensional figure under consideration is a polyhedron, that is, it is formed by a set of intersecting planes, it is characterized by a certain number of vertices, edges and faces. They are all elements of a prism.
In the middle of the 18th century, the Swiss mathematician Leonhard Euler established a connection between the number of basic elements of a polyhedron. This relationship is written with the following simple formula:
Number of edges=number of vertices + number of faces - 2
For any prism, this equality is true. Let's give an example of its use. Suppose there is a regular quadrangular prism. She is pictured below.
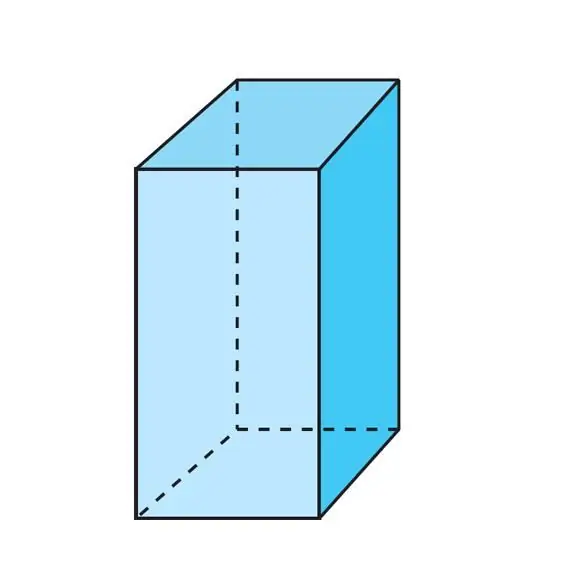
It can be seen that the number of vertices for it is 8 (4 for each quadrangular base). The number of sides or faces is 6 (2 bases and 4 side rectangles). Then the number of edges for it will be:
Number of ribs=8 + 6 - 2=12
All of them can be counted if you refer to the same picture. Eight edges lie at the bases, and four edges are perpendicular to these bases.
Full classification of prisms
It is important to understand this classification so that you do not get confused in the terminology later and use the correct formulas to calculate, for example, the surface area or volume of figures.
For any prism of arbitrary shape, 4 features can be distinguished that will characterize it. Let's list them:
- By the number of corners of the polygon at the base: triangular, pentagonal, octagonal and so on.
- Polygon type. It may be right or wrong. For example, a right triangle is irregular, but an equilateral triangle is correct.
- According to the type of polygon convexity. It can be concave or convex. Convex prisms are the most common.
- At the angles between the bases and side parallelograms. If all these angles are equal to 90o, then they speak of a right prism, if not all of them are right, then such a figure is called oblique.
Of all these points, I would like to dwell on the last one. A straight prism is also called a rectangular prism. This is due to the fact that for it parallelograms are rectangles in the general case (in some cases they can be squares).
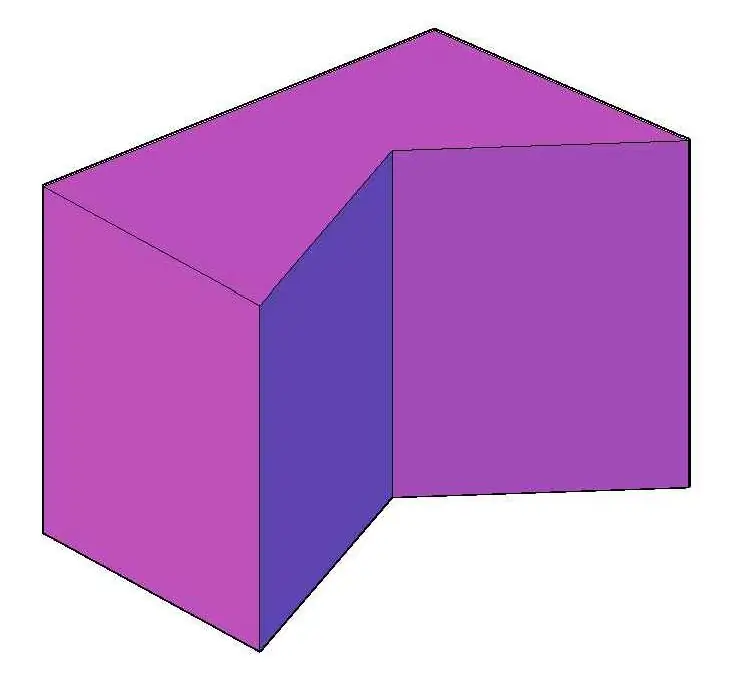
For example, the figure above shows a pentagonal concave rectangular or straight figure.
Regular quadrangular prism
The base of this prism is a regular quadrilateral, that is, a square. The figure above has already shown what this prism looks like. In addition to the two squares that herlimit top and bottom, it also includes 4 rectangles.
Let's denote the side of the base of a regular quadrangular prism by the letter a, the length of its side edge will be denoted by the letter c. This length is also the height of the figure. Then the area of the entire surface of this prism is expressed by the formula:
S=2a2+ 4ac=2a(a + 2c)
Here the first term reflects the contribution of the bases to the total area, the second term is the area of the lateral surface.
Taking into account the introduced notation for the lengths of the sides, we write the formula for the volume of the figure in question:
V=a2c
That is, the volume is calculated as the product of the area of the square base and the length of the side edge.
Cube shape
Everyone knows this ideal three-dimensional figure, but few people thought that it is a regular quadrangular prism, the side of which is equal to the length of the side of the square base, that is, c=a.
For a cube, the formulas for the total surface area and volume will take the form:
S=6a2
V=a3
Since a cube is a prism consisting of 6 identical squares, any parallel pair of them can be considered a base.
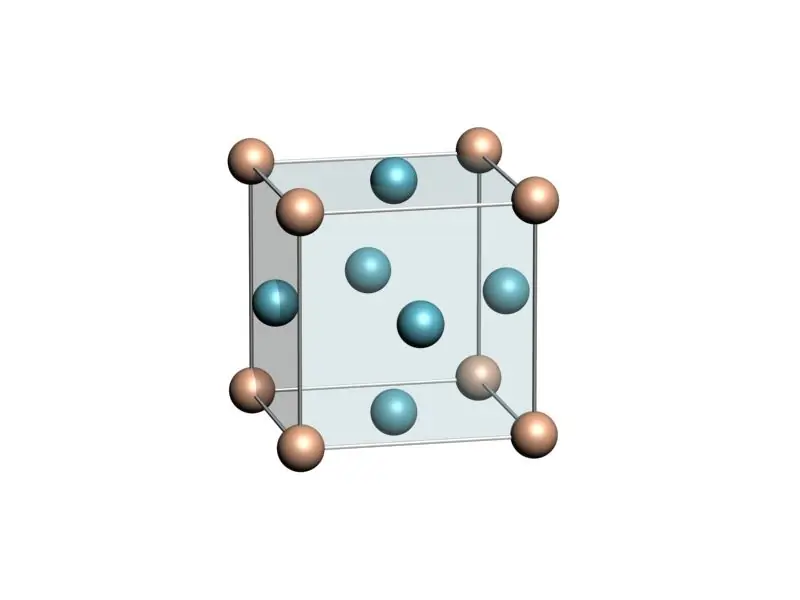
Cube is a highly symmetrical figure, which in nature is realized in the form of crystal lattices of many metallic materials and ionic crystals. For example, lattices of gold, silver, copper and tables alts are cubic.






