At the word "infinity" each person has his own associations. Many draw in their imagination the sea that goes beyond the horizon, while others have a picture of an endless starry sky before their eyes. Mathematicians, accustomed to operating with numbers, imagine the infinity in a completely different way. For many centuries they have been trying to find the largest of the physical quantities required for measuring. One of them is the Graham number. How many zeros are in it and what it is used for, this article will tell.

Infinitely large number
In mathematics, this is the name of such a variable x , if for any given positive number M one can specify a natural number N such that for all numbers n greater than N the inequality |x | > M. However, no, for example, integer Z can be considered infinitely large, since it will always be less than (Z + 1).
A few words about "giants"
The largest numbers that have physical meaning are considered to be:
- 1080. This number, which is commonly called a quinquavigintillion, is used to denote the approximate number of quarks and leptons (the smallest particles) in the Universe.
- 1 Google. Such a number in the decimal system is written as a unit with 100 zeros. According to some mathematical models, from the time of the big bang to the explosion of the most massive black hole, from 1 to 1.5 googol years should pass, after which our universe will move into the last stage of its existence, i.e., we can assume that this number has a certain physical meaning.
- 8, 5 x 10185. Planck's constant is 1.616199 x 10-35 m, i.e. in decimal notation it looks like 0.00000000000000000000000000000616199 m. There are about 1 googol Planck length in an inch. It is estimated that about 8.5 x 10185 Planck lengths can fit in our entire universe.
- 277 232 917 - 1. This is the largest known prime number. If its binary notation has a fairly compact form, then in order to depict it in decimal form, it will take no less than 13 million characters. It was found in 2017 as part of a project to search for Mersenne numbers. If enthusiasts continue to work in this direction, then at the current level of development of computer technology, in the near future they are unlikely to be able to find a Mersenne number an order of magnitude larger than 277 232 917 - 1, although suchthe lucky winner will receive US$150,000.
- Hugoplex. Here we just take 1 and add zeros after it in the amount of 1 googol. You can write this number as 10^10^100. It is impossible to represent it in decimal form, because if the entire space of the Universe is filled with pieces of paper, on each of which 0 would be written with a “Word” font size of 10, then in this case only half of all 0 after 1 would be obtained for the googolplex number.
- 10^10^10^10^10^1.1. This is a number showing the number of years after which, according to the Poincaré theorem, our Universe, as a result of random quantum fluctuations, will return to a state close to today.
How Graham's numbers came about
In 1977, the well-known popularizer of science Martin Gardner published an article in Scientific American concerning Graham's proof of one of the problems of Ramse's theory. In it, he called the boundary set by the scientist the largest number ever used in serious mathematical reasoning.
Who is Ronald Lewis Graham
The scientist, now in his 80s, was born in California. In 1962, he received a Ph. D in mathematics from the University of Berkeley. He worked at Bell Labs for 37 years and later moved to AT&T Labs. The scientist actively collaborated with one of the greatest mathematicians of the 20th century, Pal Erdős, and is the winner of many prestigious awards. Graham's scientific bibliography contains more than 320 scientific papers.
In the mid-70s, the scientist was interested in the problem associated with the theoryRamsey. In its proof, the upper bound of the solution was determined, which is a very large number, subsequently named after Ronald Graham.
Hypercube problem
To understand the essence of the Graham number, you must first understand how it was obtained.
The scientist and his colleague Bruce Rothschild were solving the following problem:
There is an n-dimensional hypercube. All pairs of its vertices are connected in such a way that a complete graph with 2vertices is obtained. Each of its edges is colored either blue or red. It was required to find the minimum number of vertices that a hypercube should have so that each such coloring contains a complete monochromatic subgraph with 4 vertices lying in the same plane.

Decision
Graham and Rothschild proved that the problem has a solution N' satisfying the condition 6 ⩽ N' ⩽N where N is a well-defined, very large number.
The lower bound for N was subsequently refined by other scientists, who proved that N must be greater than or equal to 13. Thus, the expression for the smallest number of vertices of a hypercube that satisfies the conditions presented above became 13 ⩽ N'⩽ N.
Knuth's arrow notation
Before defining the Graham number, you should familiarize yourself with the method of its symbolic representation, since neither decimal nor binary notation is absolutely suitable for this.
Currently, Knuth's arrow notation is used to represent this quantity. According to her:
ab=a "up arrow" b.
For the operation of multiple exponentiation, the entry was introduced:
a "up arrow" "up arrow" b=ab="a tower consisting of a in the amount of b pieces."
And for pentation, i.e. symbolic designation of repeated exponentiation of the previous operator, Knuth already used 3 arrows.
Using this notation for the Graham number, we have "arrow" sequences nested in each other, in the amount of 64 pcs.
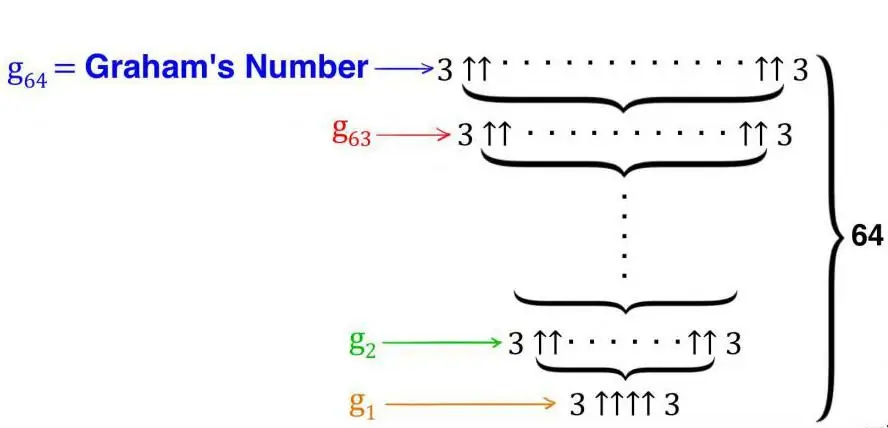
Scale
Their famous number, which excites the imagination and expands the boundaries of human consciousness, taking it beyond the limits of the Universe, Graham and his colleagues obtained it as an upper bound for the number N in the proof of the hypercube problem presented above. It is extremely difficult for an ordinary person to imagine how large its scale is.
The question of the number of characters, or as it is sometimes mistakenly said, zeros in Graham's number, is of interest to almost everyone who hears about this value for the first time.
Suffice it to say that we are dealing with a rapidly growing sequence that consists of 64 members. Even its first term is impossible to imagine, since it consists of n "towers", consisting of 3-to. Already its "lower floor" of 3 triples is equal to 7,625,597,484,987, i.e., it exceeds 7 billion, which is to say about the 64th floor (not a member!). Thus, it is currently impossible to say exactly what the Graham number is, since it is not enough to calculate it.the combined power of all the computers that exist on Earth today.

Record broken?
In the process of proving Kruskal's theorem, Graham's number was “thrown off its pedestal”. The scientist proposed the following problem:
There is an infinite sequence of finite trees. Kruskal proved that there always exists a section of some graph, which is both a part of a larger graph and its exact copy. This statement does not raise any doubts, since it is obvious that there will always be an exactly repeating combination at infinity
Later, Harvey Friedman somewhat narrowed this problem by considering only such acyclic graphs (trees) that for a particular one with coefficient i there are at most (i + k) vertices. He decided to find out what the number of acyclic graphs should be, so that with this method of their task it would always be possible to find a subtree that would be embedded in another tree.
As a result of research on this issue, it was found that N, depending on k, grows at a tremendous speed. In particular, if k=1, then N=3. However, at k=2, N already reaches 11. The most interesting thing begins when k=3. In this case, N rapidly "takes off" and reaches a value that is many times greater than the Graham number. To imagine how large it is, it is enough to write down the number calculated by Ronald Graham in the form of G64 (3). Then the Friedman-Kruskal value (rev. FinKraskal(3)), will be of the order of G(G(187196)). In other words, a mega-value is obtained, which is infinitely largeran unimaginably large Graham number. At the same time, even it will be less than infinity by a gigantic number of times. It makes sense to talk about this concept in more detail.

Infinity
Now that we have explained what the Graham number on the fingers is, we should understand the meaning that has been and is being invested in this philosophical concept. After all, “infinity” and “an infinitely large number” can be considered identical in a certain context.
The greatest contribution to the study of this issue was made by Aristotle. The great thinker of antiquity divided infinity into potential and actual. By the latter, he meant the reality of the existence of infinite things.
According to Aristotle, the sources of ideas about this fundamental concept are:
- time;
- separation of values;
- the concept of the border and the existence of something beyond it;
- the inexhaustibility of creative nature;
- thinking that has no limits.
In the modern interpretation of infinity, you can not specify a quantitative measure, so the search for the largest number can go on forever.
Conclusion
Can the metaphor "Gaze into infinity" and Graham's number be considered synonymous in some sense? Rather yes and no. Both are impossible to imagine, even with the strongest imagination. However, as already mentioned, it cannot be considered "the most, the most." Another thing is that at the moment, values greater than the Graham number do not have an establishedphysical sense.
Also, it does not have the properties of an infinite numberlike:
- ∞ + 1=∞;
- there is an infinite number of both odd and even numbers;
- ∞ - 1=∞;
- the number of odd numbers is exactly half of all numbers;
- ∞ + ∞=∞;
- ∞/2=∞.

To summarize: Graham's number is the largest number in the practice of mathematical proof, according to the Guinness Book of Records. However, there are numbers that are many times greater than this value.
Most likely, in the future there will be a need for even greater "giants", especially if a person goes beyond our solar system or invents something unimaginable at the current level of our consciousness.






