Since the force of gravity acts on a liquid, a liquid substance has weight. Weight is the force with which it presses on the support, that is, on the bottom of the vessel into which it is poured. Pascal's law says: the pressure on the fluid is transmitted to any point in it, without changing its strength. How to calculate the pressure of a liquid on the bottom and walls of a vessel? We will understand the article using illustrative examples.
Experience
Let's imagine that we have a cylindrical vessel filled with liquid. We denote the height of the liquid layer h, the area of the bottom of the vessel - S, and the density of the liquid - ρ. The desired pressure is P. It is calculated by dividing the force acting at an angle of 90 ° to the surface by the area of \u200b\u200bthis surface. In our case, the surface is the bottom of the container. P=F/S.

The force of liquid pressure on the bottom of the vessel is the weight. It is equal to the force of pressure. Our fluid is stationary, so weight equals gravity(Fstrand) acting on the liquid, and hence the pressure force (F=Fstrength). Fheavy is found as follows: multiply the mass of the liquid (m) by the acceleration of free fall (g). The mass can be found if it is known what is the density of the liquid and what is its volume in the vessel. m=ρ×V. The vessel has a cylindrical shape, so we will find its volume by multiplying the base area of the cylinder by the height of the liquid layer (V=S×h).
Calculation of liquid pressure at the bottom of the vessel
Here are the quantities we can calculate: V=S×h; m=ρ×V; F=m×g. Let's substitute them into the first formula and get the following expression: P=ρ×S×h×g/S. Let us reduce the area S in the numerator and denominator. It will disappear from the formula, which means that the pressure on the bottom does not depend on the area of the vessel. In addition, it does not depend on the shape of the container.
The pressure that a liquid creates on the bottom of a vessel is called hydrostatic pressure. "Hydro" is "water" and static is because the fluid is still. Using the formula obtained after all transformations (P=ρ×h×g), determine the pressure of the liquid at the bottom of the vessel. It can be seen from the expression that the denser the liquid, the greater its pressure on the bottom of the vessel. Let's analyze in more detail what the value h.
Pressure in the liquid column
Let's say we increased the bottom of the vessel by a certain amount, added additional space for the liquid. If we place a fish in a container, will the pressure on it be the same in the vessel from the previous experiment and in the second, enlarged one? Will the pressure change from what is still under the fishis there water? No, because there is a certain layer of liquid on top, gravity acts on it, which means that water has weight. What's below is irrelevant. Therefore, we can find the pressure in the very thickness of the liquid, and h is the depth. It is not necessarily the distance to the bottom, the bottom can be lower.

Let's imagine that we turned the fish 90°, leaving it at the same depth. Will this change the pressure on her? No, because at depth it is the same in all directions. If we bring a fish close to the vessel wall, will the pressure on it change if it stays at the same depth? No. In all cases, the pressure at depth h will be calculated using the same formula. Hence, this formula allows us to find the pressure of the liquid on the bottom and walls of the vessel at a depth h, i.e., in the thickness of the liquid. The deeper, the bigger it is.
Pressure in inclined vessel
Let's imagine that we have a tube about 1 m long. We pour liquid into it so that it is completely filled. Let's take exactly the same tube, filled to the brim, and place it at an angle. The vessels are identical and filled with the same liquid. Therefore, the mass and weight of the liquid in both the first and second tubes are equal. Will the pressure be the same at the points located at the bottom of these containers? At first glance, it seems that the pressure P1 is equal to P2, since the mass of the liquids is the same. Let's assume this is the case and let's do an experiment to check it out.
Connect the lower parts of these tubes with a small tube. If aour assumption that P1 =P2 is correct, will the liquid flow somewhere? No, because its particles will be affected by forces in the opposite direction, which will compensate each other.
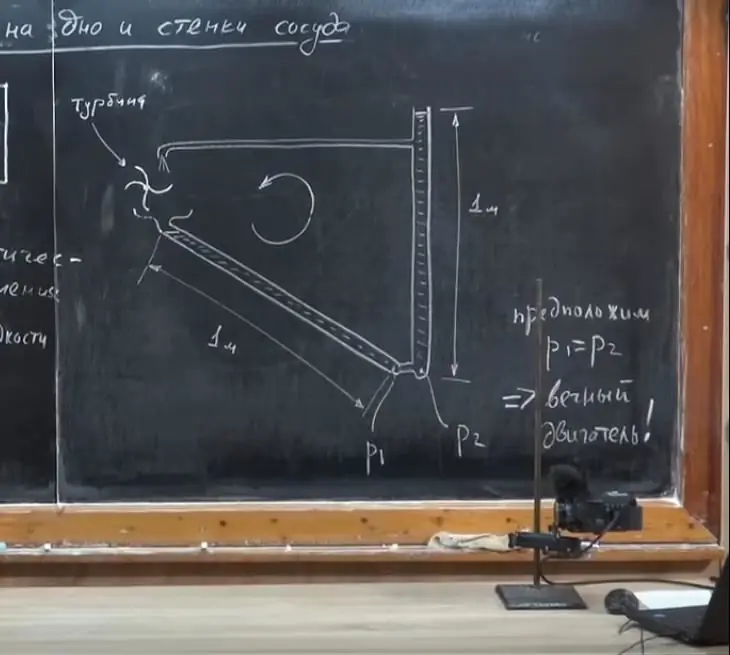
Let's attach a funnel to the top of the sloping tube. And on the vertical tube we make a hole, insert a tube into it, which bends down. The pressure at the level of the hole is greater than at the very top. This means that the liquid will flow through a thin tube and fill the funnel. The mass of liquid in the inclined tube will increase, the liquid will flow from the left tube to the right one, then it will rise and circulate in a circle.
And now we will install a turbine over the funnel, which we will connect to an electric generator. Then this system will generate electricity on its own, without any intervention. She will work non-stop. It would seem that this is the "perpetual motion machine". However, as early as the 19th century, the French Academy of Sciences refused to accept any such projects. The law of conservation of energy says that it is impossible to create a "perpetual motion machine". So our assumption that P1 =P2 is wrong. Actually P1< P2. How, then, to calculate the pressure of the liquid on the bottom and walls of the vessel in a tube that is located at an angle?
Height of liquid column and pressure
To find out, let's do the following thought experiment. Take a vessel filled with liquid. We place two tubes in it frommetal mesh. We will place one vertically, and the other - obliquely, so that its lower end will be at the same depth as the bottom of the first tube. Since the containers are at the same depth h, the pressure of the liquid on the bottom and walls of the vessel will also be the same.

Now close up all the holes in the tubes. Due to the fact that they have become solid, will the pressure in their lower parts change? No. Although the pressure is the same, and the vessels are equal in size, the mass of liquid in a vertical tube is less. The depth at which the bottom of the tube is located is called the height of the liquid column. Let's give a definition to this concept: it is the distance measured vertically from the free surface to a given point in the liquid. In our example, the height of the liquid column is the same, so the pressure is the same. In the previous experiment, the height of the liquid column in the right tube is greater than in the left one. Therefore, the pressure P1 is less than P2.






