When studying stereometry, one of the main topics is "Cylinder". The lateral surface area is considered, if not the main, then an important formula in solving geometric problems. However, it is important to remember definitions that will help you navigate through examples and when proving various theorems.
Cylinder concept
First we need to consider a few definitions. Only after studying them can one begin to consider the question of the formula for the area of the lateral surface of a cylinder. Based on this entry, other expressions can be calculated.
- A cylindrical surface is understood as a plane described by a generatrix, moving and remaining parallel to a given direction, sliding along an existing curve.
- There is also a second definition: a cylindrical surface is formed by a set of parallel lines intersecting a given curve.
- Generative is conventionally called the height of the cylinder. When it moves around an axis passing through the center of the base,the designated geometric body is obtained.
- Under the axis is meant a straight line passing through both bases of the figure.
- A cylinder is a stereometric body bounded by an intersecting lateral surface and 2 parallel planes.
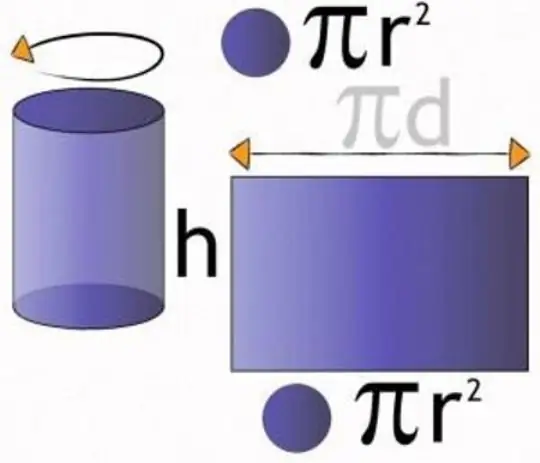
There are varieties of this three-dimensional figure:
- Circular is a cylinder whose guide is a circle. Its main components are the radius of the base and the generatrix. The latter is equal to the height of the figure.
- There is a straight cylinder. It got its name due to the perpendicularity of the generatrix to the bases of the figure.
- The third kind is a beveled cylinder. In textbooks, you can also find another name for it - "circular cylinder with a beveled base." This figure defines the radius of the base, the minimum and maximum heights.
- An equilateral cylinder is understood as a body having equal height and diameter of a circular plane.
Symbols
Traditionally, the main "components" of a cylinder are called as follows:
- The radius of the base is R (it also replaces the same value of a stereometric figure).
- Generative - L.
- Height - H.
- Base area - Sbase (in other words, you need to find the specified circle parameter).
- Beveled cylinder heights - h1, h2 (minimum and maximum).
- Side surface area - Sside (if you expand it, you getsort of a rectangle).
- The volume of a stereometric figure - V.
- Total surface area - S.
“Components” of a stereometric figure
When studying a cylinder, the lateral surface area plays an important role. This is due to the fact that this formula is included in several other, more complex ones. Therefore, it is necessary to be well versed in theory.
The main components of the figure are:
- Side surface. As you know, it is obtained due to the movement of the generatrix along a given curve.
- Full surface includes existing bases and side plane.
- The section of a cylinder, as a rule, is a rectangle located parallel to the axis of the figure. Otherwise, it is called a plane. It turns out that the length and width are part-time components of other figures. So, conditionally, the lengths of the section are generators. Width - parallel chords of a stereometric figure.
- Axial section means the location of the plane through the center of the body.
- And finally, the final definition. A tangent is a plane passing through the generatrix of the cylinder and at right angles to the axial section. In this case, one condition must be met. The specified generatrix must be included in the plane of the axial section.
Basic formulas for working with a cylinder
In order to answer the question of how to find the surface area of a cylinder, it is necessary to study the main "components" of a stereometric figure and the formulas for finding them.

These formulas differ in that first the expressions for the beveled cylinder are given, and then for the straight one.

Deconstructed Examples
Task 1.
It is necessary to know the area of the lateral surface of the cylinder. The diagonal of the section AC=8 cm is given (moreover, it is axial). When in contact with the generatrix, it turns out <ACD=30°
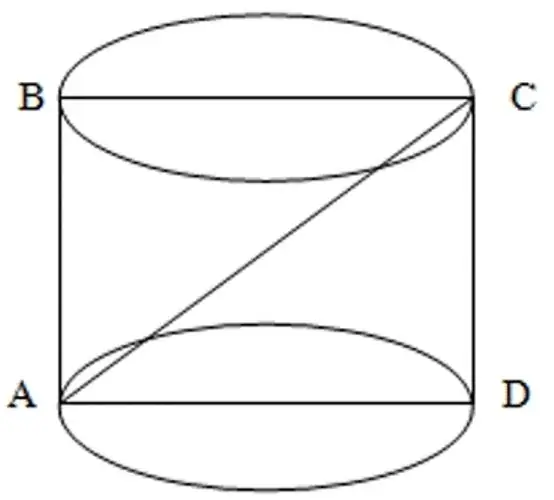
Decision. Since the values of the diagonal and the angle are known, then in this case:
CD=ACcos 30°
Comment. Triangle ACD, in this particular example, is a right triangle. This means that the quotient of dividing CD and AC=the cosine of the given angle. The value of trigonometric functions can be found in a special table.
Similarly, you can find the value of AD:
AD=ACsin 30°
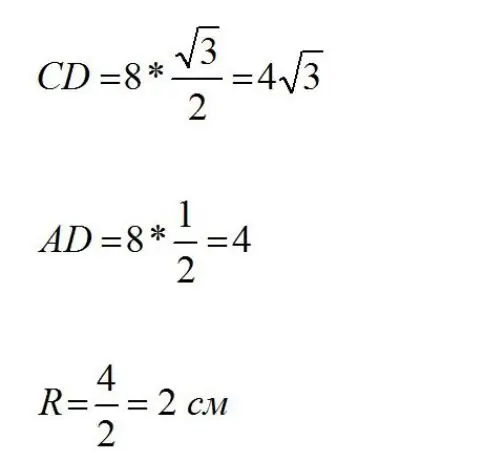
Now you need to calculate the desired result using the following formulation: the area of the lateral surface of the cylinder is equal to twice the result of multiplying "pi", the radius of the figure and its height. Another formula should also be used: the area of the base of the cylinder. It is equal to the result of multiplying "pi" by the square of the radius. And finally, the last formula: total surface area. It is equal to the sum of the previous two areas.
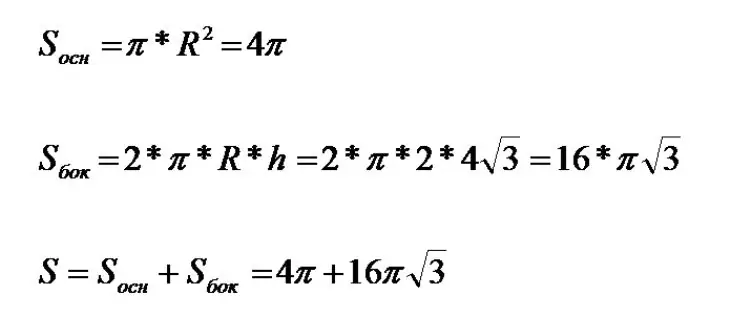
Task 2.
Cylinders are given. Their volume=128n cm³. Which cylinder has the smallestfull surface?
Decision. First you need to use the formulas for finding the volume of a figure and its height.
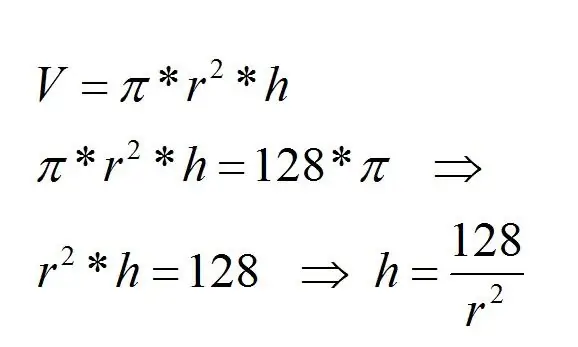
Since the total surface area of a cylinder is known from theory, its formula must be applied.

If we consider the resulting formula as a function of the area of the cylinder, then the minimum "indicator" will be reached at the extremum point. To get the last value, you need to use differentiation.
Formulas can be viewed in a special table for finding derivatives. In the future, the result found is equated to zero and the solution of the equation is found.
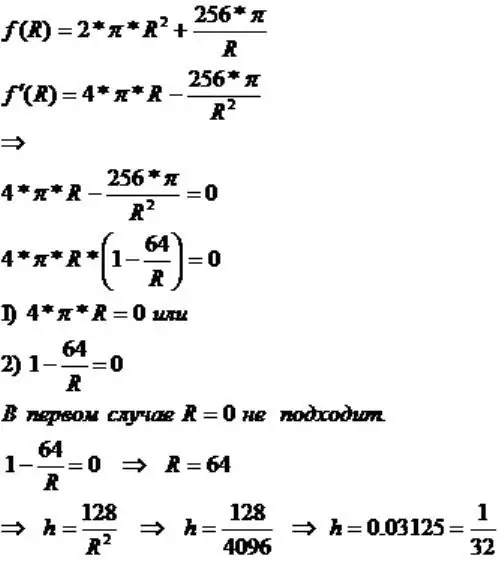
Answer: Smin will be reached at h=1/32 cm, R=64 cm.
Problem 3.
Given a stereometric figure - a cylinder and a section. The latter is carried out in such a way that it is parallel to the axis of the stereometric body. The cylinder has the following parameters: VK=17 cm, h=15 cm, R=5 cm. It is necessary to find the distance between the section and the axis.

Decision.
Since the cross section of a cylinder is understood to be VSCM, i.e. a rectangle, its side VM=h. WMC needs to be considered. The triangle is rectangular. Based on this statement, we can deduce the correct assumption that MK=BC.
VK²=VM² + MK²
MK²=VK² - VM²
MK²=17² - 15²
MK²=64
MK=8
From here we can conclude that MK=BC=8 cm.
The next step is to draw a section through the base of the figure. It is necessary to consider the resulting plane.
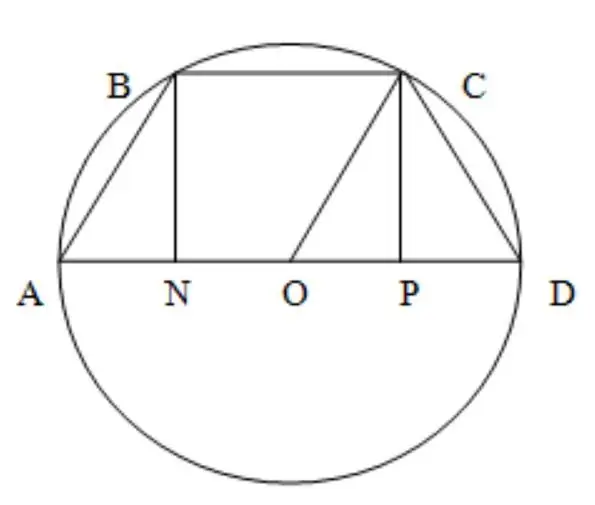
AD - diameter of a stereometric figure. It is parallel to the section mentioned in the problem statement.
BC is a straight line located on the plane of the existing rectangle.
ABCD is a trapezoid. In a particular case, it is considered isosceles, since a circle is described around it.
If you find the height of the resulting trapezoid, you can get the answer given at the beginning of the problem. Namely: finding the distance between the axis and the section drawn.
To do this, you need to find the values of AD and OS.

Answer: the section is located 3 cm from the axis.
Problems to consolidate the material
Example 1.
Cylinder given. The lateral surface area is used in the further solution. Other options are known. The area of the base is Q, the area of the axial section is M. It is necessary to find S. In other words, the total area of the cylinder.
Example 2.
Cylinder given. The lateral surface area must be found in one of the steps of solving the problem. It is known that cm, radius=2 cm. It is necessary to find the total area of a stereometric figure.






