The area of the lateral surface and the volume of a truncated pyramid: formulas and an example of solving a typical problem

2024 Author: Angel Austin | [email protected]. Last modified: 2024-01-02 17:39

When studying the properties of figures in three-dimensional space within the framework of stereometry, one often has to solve problems to determine the volume and surface area. In this article, we will show how to calculate the volume and lateral surface area for a truncated pyramid using well-known formulas.

Pyramid in geometry

In geometry, an ordinary pyramid is a figure in space, which is built on some flat n-gon. All its vertices are connected to one point located outside the plane of the polygon. For example, here is a photo showing a pentagonal pyramid.

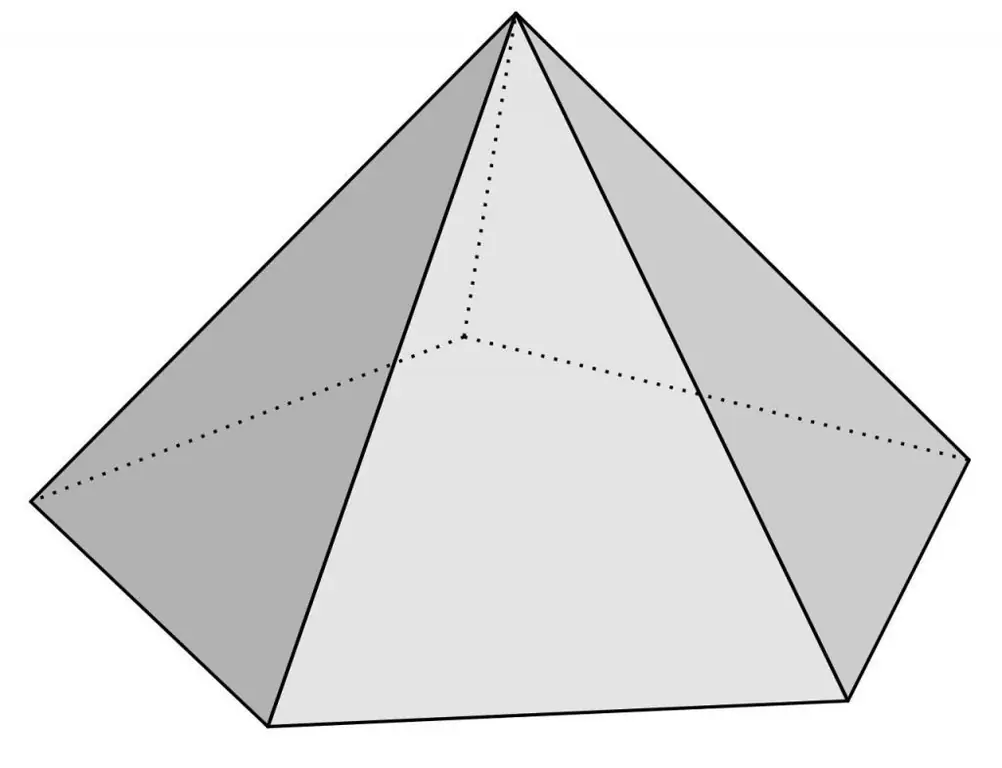
This figure is formed by faces, vertices and edges. The pentagonal face is called the base. The remaining triangular faces form the side surface. The intersection point of all triangles is the main vertex of the pyramid. If a perpendicular is lowered from it to the base, then two options for the position of the intersection point are possible:

• in the geometric center, then the pyramid is called a straight line;
• not ingeometric center, then the figure will be oblique.

Further we will consider only straight figures with a regular n-gonal base.

What is this figure - a truncated pyramid?

To determine the volume of a truncated pyramid, it is necessary to clearly understand which figure is specifically in question. Let's clarify this issue.

Suppose we take a cutting plane that is parallel to the base of an ordinary pyramid and cut off a part of the side surface with it. If this operation is done with the pentagonal pyramid shown above, you will get such a figure as in the figure below.

From the photo it can be seen that this pyramid already has two bases, and the top one is similar to the bottom one, but it is smaller in size. The lateral surface is no longer represented by triangles, but by trapezoids. They are isosceles, and their number corresponds to the number of sides of the base. The truncated figure does not have a main vertex, like a regular pyramid, and its height is determined by the distance between parallel bases.

In the general case, if the figure under consideration is formed by n-gonal bases, it has n+2 faces or sides, 2n vertices and 3n edges. That is, the truncated pyramid is a polyhedron.

Formula for the volume of a truncated pyramid

Recall that the volume of an ordinary pyramid is 1/3 of the product of its height and base area. This formula is not suitable for a truncated pyramid, since it has two bases. And its volumewill always be less than the same value for the regular figure from which it is derived.

Without going into the mathematical details of obtaining the expression, we present the final formula for the volume of a truncated pyramid. It is written as follows:

V=1/3h(S₁+ S₂+ √(S₁ S₂₎₎

Here S₁ and S_{2 are the areas of the lower and upper bases, respectively, h is the height of the figure. The written expression is valid not only for a straight regular truncated pyramid, but also for any figure of this class. Moreover, regardless of the type of base polygons. The only condition limiting the use of the expression for V is the need for the bases of the pyramid to be parallel to each other.}

Several important conclusions can be drawn by studying the properties of this formula. So, if the area of the upper base is zero, then we come to the formula for V of an ordinary pyramid. If the areas of the bases are equal to each other, then we get the formula for the volume of the prism.

How to determine the lateral surface area?

Knowing the characteristics of a truncated pyramid requires not only the ability to calculate its volume, but also to know how to determine the area of the lateral surface.

Truncated pyramid consists of two types of faces:

• isosceles trapezoids;
• polygonal bases.

If there is a regular polygon in the bases, then the calculation of its area does not represent largedifficulties. To do this, you only need to know the length of the side a and their number n.

In the case of a lateral surface, the calculation of its area involves determining this value for each of the n trapezoids. If the n-gon is correct, then the formula for the lateral surface area becomes:

S_b=h_bn(a₁+a_2)/2

Here h_b is the height of the trapezoid, which is called the figure's apoteme. The quantities a₁ and a_{2are the lengths of the sides of regular n-gonal bases.}

For every regular n-gonal truncated pyramid, the apotema h_b can be uniquely defined through the parameters a₁ and a_{2and the height h of the shape.}

The task of calculating the volume and area of a figure

Given a regular triangular truncated pyramid. It is known that its height h is 10 cm, and the lengths of the sides of the bases are 5 cm and 3 cm. What is the volume of the truncated pyramid and the area of its lateral surface?

First, let's calculate the value V. To do this, find the areas of equilateral triangles located at the bases of the figure. We have:

S₁=√3/4a₁²=√3/4 5²=10.825cm^2;

S₂=√3/4a₂²=√3/4 3²=3.897 cm²

Substitute the data into the formula for V, we get the desired volume:

V=1/310(10, 825 + 3, 897 + √(10, 825 3, 897)) ≈ 70.72 cm3

To determine the side surface, you should knowapothem length h_{b. Considering the corresponding right-angled triangle inside the pyramid, we can write the equality for it:}

h_b=√((√3/6(a₁- a₂))²+ h^{2) ≈ 10.017 cm}

The value of the apothem and the sides of the triangular bases are substituted into the expression for S_{b and we get the answer:}

S_b=h_bn(a₁+a₂)/2=10.0173(5+3)/2 ≈ 120.2cm²

Thus, we answered all the questions of the problem: V ≈ 70.72 cm³, S_b ≈ 120.2 cm ^2.