How to calculate the area of a pyramid: base, side and full?

2024 Author: Angel Austin | [email protected]. Last modified: 2023-12-17 05:14

When preparing for the exam in mathematics, students have to systematize their knowledge of algebra and geometry. I would like to combine all known information, for example, how to calculate the area of a pyramid. Moreover, starting from the base and side faces to the entire surface area. If the situation is clear with the side faces, since they are triangles, then the base is always different.

How to find the area of the base of the pyramid?

It can be absolutely any shape: from an arbitrary triangle to an n-gon. And this base, in addition to the difference in the number of angles, can be a regular figure or an incorrect one. In the USE tasks of interest to schoolchildren, there are only tasks with the correct figures at the base. Therefore, we will only talk about them.

Regular Triangle

That is equilateral. One in which all sides are equal and denoted by the letter "a". In this case, the area of the base of the pyramid is calculated by the formula:

S=(a2√3) / 4.

Square

The formula for calculating its area is the simplest,here "a" is the side again:

S=a2.

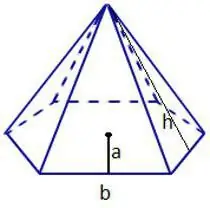
Arbitrary regular n-gon

The side of a polygon has the same designation. For the number of corners, the Latin letter n is used.

S=(na2) / (4tg (180º/n)).

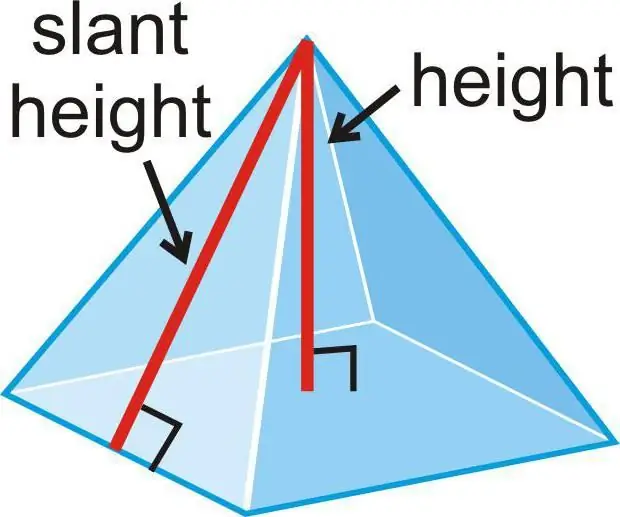
How to calculate lateral and total surface area?

Since the base is a regular figure, all sides of the pyramid are equal. Moreover, each of them is an isosceles triangle, since the side edges are equal. Then, in order to calculate the lateral area of \u200b\u200bthe pyramid, you need a formula consisting of the sum of identical monomials. The number of terms is determined by the number of sides of the base.

The area of an isosceles triangle is calculated by the formula in which half the product of the base is multiplied by the height. This height in the pyramid is called apothem. Its designation is "A". The general formula for lateral surface area is:

S=½ PA, where P is the perimeter of the base of the pyramid.

There are situations when the sides of the base are not known, but the side edges (c) and the flat angle at its vertex (α) are given. Then it is supposed to use this formula to calculate the lateral area of the pyramid:

S=n/2in2 sin α.

Problem 1

Condition. Find the total area of the pyramid if its base is an equilateral triangle with a side of 4 cm, and the apothem is √3 cm.

Decision. HisYou need to start by calculating the perimeter of the base. Since this is a regular triangle, then P \u003d 34 \u003d 12 cm. Since the apothem is known, you can immediately calculate the area of \u200b\u200bthe entire lateral surface: ½12√3=6√3 cm 2.

For a triangle at the base, you get the following area value: (4²√3) / 4=4√3 cm^2.

To determine the total area, you need to add the two resulting values: 6√3 + 4√3=10√3 cm2.

Answer. 10√3 cm2.

Problem 2

Condition. There is a regular quadrangular pyramid. The length of the side of the base is 7 mm, the side edge is 16 mm. You need to know its surface area.

Decision. Since the polyhedron is quadrangular and regular, then its base is a square. Having learned the areas of the base and side faces, it will be possible to calculate the area of \u200b\u200bthe pyramid. The formula for the square is given above. And at the side faces, all sides of the triangle are known. Therefore, you can use Heron's formula to calculate their areas.

The first calculations are simple and lead to this number: 49 mm². For the second value, you will need to calculate the semi-perimeter: (7 + 162): 2=19.5 mm. Now you can calculate the area of an isosceles triangle: √(19.5(19.5-7)(19.5-16)²)=√2985.9375=54.644 mm ^{2. There are only four such triangles, so when calculating the final number, you will need to multiply it by 4.}

It turns out: 49 + 454, 644=267, 576 mm2.

Answer. Desired value 267, 576mm2.

Problem 3

Condition. For a regular quadrangular pyramid, you need to calculate the area. It knows the side of the square - 6 cm and the height - 4 cm.

Decision. The easiest way is to use the formula with the product of the perimeter and the apothem. The first value is easy to find. The second is a little more difficult.

We'll have to remember the Pythagorean theorem and consider a right triangle. It is formed by the height of the pyramid and the apothem, which is the hypotenuse. The second leg is equal to half the side of the square, since the height of the polyhedron falls into its middle.

The desired apothem (the hypotenuse of a right triangle) is √(3² + 4^{2)=5 (cm).}

Now you can calculate the required value: ½(46)5+6²=96 (see^2).

Answer. 96 cm2.

Problem 4

Condition. Given a regular hexagonal pyramid. The sides of its base are 22 mm, the side ribs are 61 mm. What is the lateral surface area of this polyhedron?

Decision. The reasoning in it is the same as described in problem No. 2. Only there was given a pyramid with a square at the base, and now it's a hexagon.

First of all, the area of the base is calculated using the above formula: (622²) / (4tg (180º/6))=726/(tg30º)=726 √3 cm^2.

Now you need to find out the semi-perimeter of an isosceles triangle, which is the side face. (22 + 612): 2 \u003d 72 cm. It remains to calculate the area of \u200b\u200beach suchtriangle, and then multiply it by six and add it to the one that turned out for the base.

Calculation by Heron's formula: √(72(72-22)(72-61)²)=√435600=660 cm² . Calculations that will give the lateral surface area: 6606=3960 cm². It remains to add them up to find out the entire surface: 5217, 47≈5217 cm^2.

Answer. Base - 726√3cm², side surface - 3960cm², total area - 5217cm^2.