Resolution is the ability of an imaging system to reproduce the details of an object, and depends on factors such as the type of lighting used, the pixel size of the sensor, and the capabilities of the optics. The smaller the detail of the subject, the higher the required resolution of the lens.
Introduction to the resolution process
The image quality of the camera depends on the sensor. Simply put, a digital image sensor is a chip inside a camera body containing millions of light-sensitive spots. The size of the camera's sensor determines how much light can be used to create an image. The larger the sensor, the better the image quality as more information is collected. Typically digital cameras advertise in the market for sensor sizes of 16mm, Super 35mm, and sometimes up to 65mm.
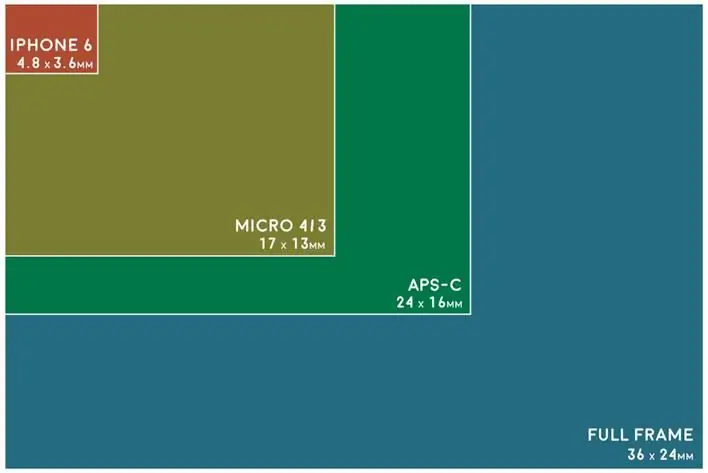
As the size of the sensor increases, the depth of field will decrease at a given aperture, as a larger counterpart requires you to get closer toobject or use a longer focal length to fill the frame. To maintain the same depth of field, the photographer must use smaller apertures.
This shallow depth of field may be desirable, especially to achieve background blur for portraiture, but landscape photography requires more depth, which is easier to capture with the flexible aperture size of compact cameras.
Dividing the number of horizontal or vertical pixels on a sensor will indicate how much space each one occupies on an object, and can be used to evaluate lens resolving power and resolve customer concerns about the device's digital image pixel size. As a starting point, it's important to understand what can actually limit the system's resolution.
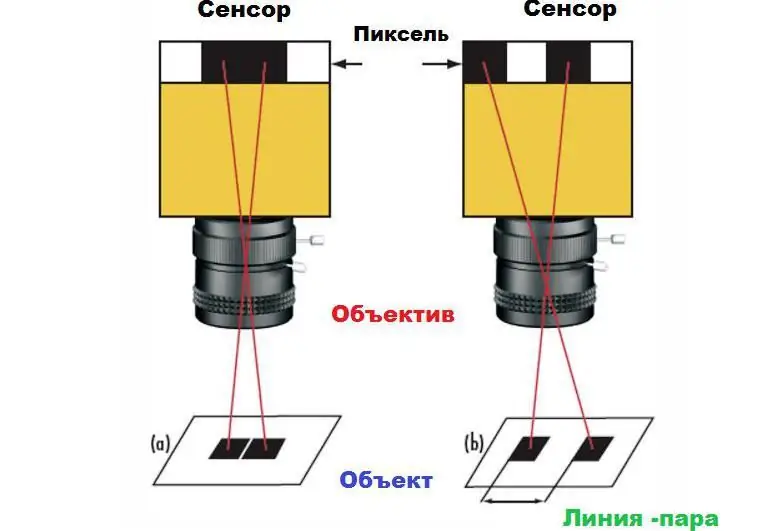
This statement can be demonstrated by the example of a pair of squares on a white background. If the squares on the camera sensor are mapped to neighboring pixels, then they will appear as one large rectangle in the image (1a) rather than two separate squares (1b). To distinguish the squares, a certain space is required between them, at least one pixel. This minimum distance is the maximum resolution of the system. The absolute limit is determined by the size of the pixels on the sensor, as well as their number.
Measuring lens characteristics
The relationship between alternating black and white squares is described as a linear pair. Typically, resolution is determined by frequency,measured in line pairs per millimeter - lp/mm. Unfortunately, lens resolution in cm is not an absolute number. At a given resolution, the ability to see the two squares as separate objects will depend on the gray scale level. The greater the gray scale separation between them and space, the more stable is the ability to resolve these squares. This division of the gray scale is known as frequency contrast.
Spatial frequency is given in lp/mm. For this reason, calculating resolution in terms of lp/mm is extremely useful when comparing lenses and determining the best choice for given sensors and applications. The first one is where the system resolution calculation starts. Starting with the sensor, it is easier to determine what lens specifications are needed to meet the requirements of the device or other applications. The highest frequency allowed by the sensor, Nyquist, is effectively two pixels or one line pair.
Definition lens resolution, also called system image space resolution, can be determined by multiplying the size in Μm by 2 to create a pair and dividing by 1000 to convert to mm:
lp/mm=1000/ (2 X pixel)
Sensors with larger pixels will have lower resolution limits. Sensors with smaller pixels will perform better according to the lens resolution formula above.
Active sensor area
You can calculate the maximum resolution for the object to beviewing. To do this, it is necessary to distinguish between indicators such as the ratio between the size of the sensor, the field of view and the number of pixels on the sensor. The size of the latter refers to the parameters of the active area of the camera sensor, usually determined by the size of its format.
However, the exact proportions will vary by aspect ratio, and nominal sensor sizes should only be used as a guideline, especially for telecentric lenses and high magnifications. The sensor size can be directly calculated from the pixel size and active pixel count to perform a lens resolution test.
The table shows the Nyquist limit associated with pixel sizes found on some very commonly used sensors.
| Pixel size (µm) | Coupled Nyquist limit (lp / mm) |
| 1, 67 | 299, 4 |
| 2, 2 | 227, 3 |
| 3, 45 | 144, 9 |
| 4, 54 | 110, 1 |
| 5, 5 | 90, 9 |
As pixel sizes decrease, the associated Nyquist limit in lp/mm increases proportionately. To determine the absolute minimum resolvable spot that can be seen on an object, the ratio of the field of view to the size of the sensor must be calculated. This is also known as primary augmentation.(PMAG) systems.
The relationship associated with the system PMAG allows for scaling the image space resolution. Typically, when designing an application, it is not specified in lp/mm, but rather in microns (µm) or fractions of an inch. You can quickly jump to the ultimate resolution of an object by using the formula above to make it easier to choose the lens resolution z. It is also important to keep in mind that there are many additional factors, and the above limitation is much less error-prone than the complexity of taking into account many factors and calculating them using equations.
Calculate focal length
The resolution of an image is the number of pixels in it. Designated in two dimensions, for example, 640X480. Calculations can be done separately for each dimension, but for simplicity this is often reduced to one. To make accurate measurements on an image, you need to use a minimum of two pixels for every smallest area you want to detect. The size of the sensor refers to a physical indicator and, as a rule, is not indicated in the passport data. The best way to determine the size of a sensor is to look at the pixel parameters on it and multiply it by the aspect ratio, in which case the resolving power of the lens solves the problems of a bad shot.
For example, the Basler acA1300-30um camera has a pixel size of 3.75 x 3.75um and a resolution of 1296 x 966 pixels. The sensor size is 3.75 µm x 1296 by 3.75 µm x 966=4.86 x 3.62 mm.
Sensor format refers to the physical size and does not depend on the pixel size. This setting is used fordetermine which lens the camera is compatible with. For them to match, the lens format must be greater than or equal to the sensor size. If a lens with a smaller aspect ratio is used, the image will experience vignetting. This causes areas of the sensor outside the edge of the lens format to become dark.
Pixels and camera selection

To see the objects in the image, there must be enough space between them so that they do not merge with neighboring pixels, otherwise they will be indistinguishable from each other. If the objects are one pixel each, the separation between them must also be at least one element, it is thanks to this that a pair of lines is formed, which actually has two pixels in size. This is one of the reasons why it is incorrect to measure the resolution of cameras and lenses in megapixels.
It's actually easier to describe the resolution capabilities of a system in terms of line pair frequency. It follows that as the pixel size decreases, the resolution increases because you can put smaller objects on smaller digital elements, have less space between them, and still resolve the distance between the subjects you shoot.
This is a simplified model of how the camera's sensor detects objects without considering noise or other parameters, and is the ideal situation.
MTF contrast charts
Most lenses are not perfect optical systems. Light passing through a lens undergoes a certain degree of degradation. The question is how to evaluate thisdegradation? Before answering this question, it is necessary to define the concept of "modulation". The latter is a measure of the contrast len at a given frequency. One could try to analyze real world images taken through a lens to determine modulation or contrast for details of different sizes or frequencies (spacing), but this is very impractical.

Instead, it is much easier to measure modulation or contrast for pairs of alternating white and dark lines. They are called rectangular lattice. The interval of lines in a rectangular wave grating is the frequency (v), for which the modulation or contrast function of the lens and the resolution are measured in cm.
The maximum amount of light will come from the light bands, and the minimum from the dark bands. If light is measured in terms of brightness (L), the modulation can be determined according to the following equation:
modulation=(Lmax - Lmin) / (Lmax + Lmin), where: Lmax is the maximum brightness of white lines in the grating, and Lmin is the minimum brightness of dark ones.
When modulation is defined in terms of light, it is often referred to as Michelson contrast because it takes the ratio of luminance from light and dark bands to measure contrast.
For example, there is a square wave grating of a certain frequency (v) and modulation, and an inherent contrast between dark and light areas reflected from this grating through the lens. Image modulation and thus lens contrast is measured for a given frequencybars (v).
The modulation transfer function (MTF) is defined as the modulation M i of the image divided by the modulation of the stimulus (object) M o, as shown in the following equation.
|
MTF (v)=M i / M 0 |
USF test grids are printed on 98% bright laser paper. Black laser printer toner has a reflectance of about 10%. So the value for M 0 is 88%. But since film has a more limited dynamic range compared to the human eye, it is safe to assume that M 0 is essentially 100% or 1. So the above formula boils down to the following more simple equation:
|
MTF (v)=Mi |
So the MTF len for a given grating frequency (v) is simply the measured grating modulation (Mi) when photographed through a lens onto film.
Microscope resolution
The resolution of a microscope objective is the shortest distance between two distinct points in its eyepiece field of view that can still be distinguished as different objects.
If two points are closer together than your resolution, they will appear fuzzy and their positions will be inaccurate. The microscope may offer high magnification, but if the lenses are of poor quality, the resulting poor resolution will degrade the image quality.
Below is the Abbe equation, where the resolutionthe power of a microscope objective z is the resolving power equal to the wavelength of the light used divided by 2 (the numerical aperture of the objective).
Several elements affect the resolution of a microscope. An optical microscope set at high magnification may produce an image that is blurred, yet it is still at the maximum resolution of the lens.
The digital aperture of a lens affects resolution. The resolving power of a microscope objective is a number that indicates the ability of a lens to collect light and resolve a point at a fixed distance from the objective. The smallest point that can be resolved by the lens is proportional to the wavelength of the collected light divided by the numerical aperture number. Therefore, a larger number corresponds to a greater ability of the lens to detect an excellent point in the field of view. The numerical aperture of the lens also depends on the amount of optical aberration correction.
Resolution of the telescope lens
Like a light funnel, a telescope is able to collect light in proportion to the area of the hole, this property is the main lens.
The diameter of the dark adapted pupil of the human eye is just under 1 centimeter, and the diameter of the largest optical telescope is 1,000 centimeters (10 meters), so that the largest telescope is one million times larger in collection area than the human eye.

This is why telescopes see fainter objects than humans. And have devices that accumulate light using electronic detection sensors for many hours.
There are two main types of telescope: lens-based refractors and mirror-based reflectors. Large telescopes are reflectors because mirrors do not have to be transparent. Telescope mirrors are among the most precise designs. The allowed error on the surface is about 1/1000 the width of a human hair - through a 10 meter hole.
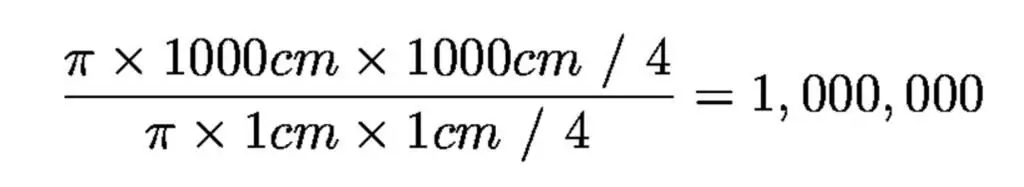
Mirrors used to be made from huge thick glass slabs to keep them from sagging. Today's mirrors are thin and flexible, but are computer controlled or otherwise segmented and aligned by computer control. In addition to the task of finding faint objects, the astronomer's goal is also to see their fine details. The degree to which details can be recognized is called resolution:
- Fuzzy images=poor resolution.
- Clear images=good resolution.
Due to the wave nature of light and phenomena called diffraction, the diameter of a telescope's mirror or lens limits its ultimate resolution relative to the diameter of the telescope. The resolution here means the smallest angular detail that can be recognized. Small values correspond to excellent image detail.
Radio telescopes must be very large to provide good resolution. Earth's atmosphere isturbulent and blurs telescope images. Terrestrial astronomers can rarely reach the maximum resolution of the apparatus. The turbulent effect of the atmosphere on a star is called vision. This turbulence causes the stars to "twinkle". To avoid these atmospheric blurs, astronomers launch telescopes into space or place them on high mountains with stable atmospheric conditions.
Examples of parameter calculation
Data to determine Canon lens resolution:
- Pixel size=3.45 µm x 3.45 µm.
- Pixels (H x V)=2448 x 2050.
- Desired field of view (horizontal)=100 mm.
- Sensor resolution limit: 1000/2x3, 45=145 lp / mm.
- Sensor Dimensions:3.45x2448/1000=8.45 mm3, 45x2050/1000=7.07 mm.
- PMAG:8, 45/100=0.0845 mm.
- Measuring lens resolution: 145 x 0.0845=12.25 lp/mm.
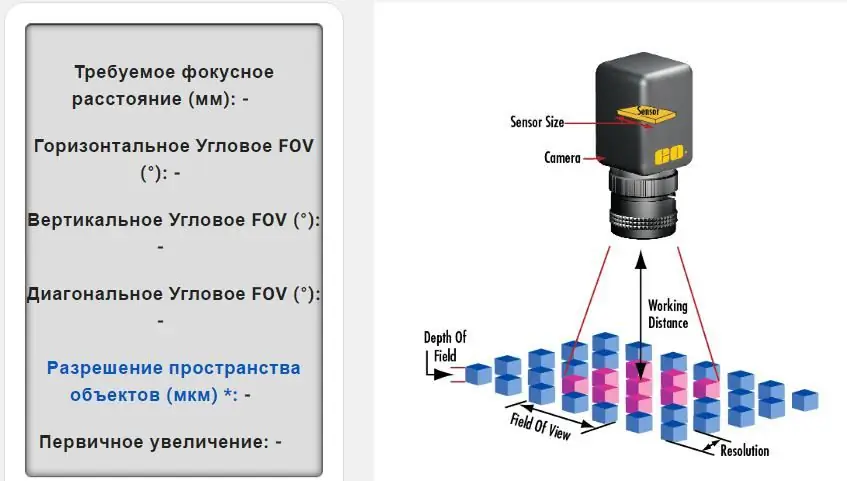
Actually, these calculations are quite complex, but they will help you create an image based on sensor size, pixel format, working distance, and field of view in mm. Calculating these values will determine the best lens for your images and application.
Problems of modern optics

Unfortunately, doubling the size of the sensor creates additional problems for lenses. One of the main parameters affecting the cost of an image lens is the format. Designing a lens for a larger format sensor requiresnumerous individual optical components, which should be larger and the transfer of the system more rigid.
A lens designed for a 1" sensor can cost five times as much as a lens designed for a ½" sensor, even if it cannot use the same specifications with limited pixel resolution. The cost component must be considered before how to determine the resolving power of a lens.
Optical imaging today faces more challenges than a decade ago. The sensors they are used with have much higher resolution requirements, and format sizes are simultaneously driven both smaller and larger, while pixel size continues to shrink.
In the past, optics never limited the imaging system, today it does. Where a typical pixel size is around 9 µm, a much more common size is around 3 µm. This 81x increase in dot density has taken its toll on optics, and while most devices are good, lens selection is now more important than ever.






