As you know, when multiplying expressions with powers, their exponents always add up (abac=ab+c). This mathematical law was derived by Archimedes, and later, in the 8th century, the mathematician Virasen created a table of integer indicators. It was they who served for the further discovery of logarithms. Examples of using this function can be found almost everywhere where it is required to simplify cumbersome multiplication to simple addition. If you spend 10 minutes reading this article, we will explain to you what logarithms are and how to work with them. Simple and accessible language.
Definition in mathematics
The logarithm is an expression of the following form: logab=c c" into which you need to raise the base "a" in order to finally get the value "b". Let's analyze the logarithm using examples, let's say there is an expression log28. How to find the answer? It's very simple, you need to find such a degree that from 2 to the required degree you get 8. Having done some calculations in your mind, we get the number 3! And it's true, because2 raised to the power of 3 gives the answer 8.
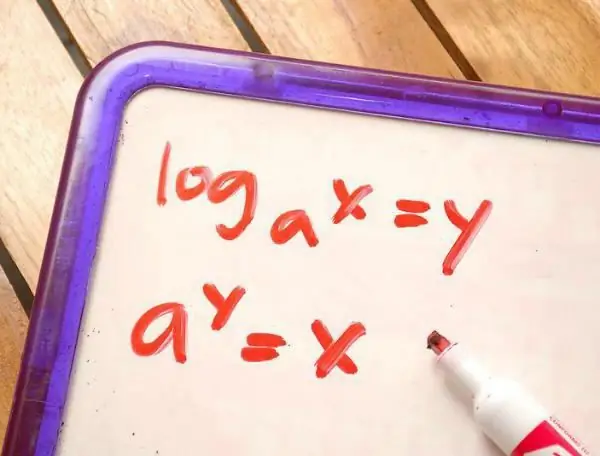
Varieties of logarithms
For many pupils and students, this topic seems complicated and incomprehensible, but in fact, logarithms are not so scary, the main thing is to understand their general meaning and remember their properties and some rules. There are three separate kinds of logarithmic expressions:
- Natural logarithm ln a, where the base is the Euler number (e=2, 7).
- Decimal logarithm lg a, where the base is the number 10.
- Logarithm of any number b to base a>1.
Each of them is solved in a standard way, including simplification, reduction and subsequent reduction to one logarithm using logarithmic theorems. To obtain the correct values of logarithms, one should remember their properties and the order of actions in solving them.
Rules and some restrictions
In mathematics, there are several rules-restrictions that are accepted as an axiom, that is, they are not negotiable and are true. For example, it is impossible to divide numbers by zero, and it is also impossible to take an even root from negative numbers. Logarithms also have their own rules, following which you can easily learn how to work even with long and capacious logarithmic expressions:
- the base of "a" must always be greater than zero, and at the same time not be equal to 1, otherwise the expression will lose its meaning, because "1" and "0" to any degree are always equal to their values;
- if a > 0, then ab>0,it turns out that "c" must also be greater than zero.
How to solve logarithms?
For example, given the task to find the answer to the equation 10x=100. It's very easy, you need to choose such a power, raising the number ten, we get 100. This, of course Well, quadratic power! 102=100.
Now let's represent this expression as a logarithmic one. We get log10100=2. When solving logarithms, all actions practically converge to finding the power to which the base of the logarithm must be entered in order to obtain a given number.
To accurately determine the value of an unknown degree, you need to learn how to work with the degree table. It looks like this:
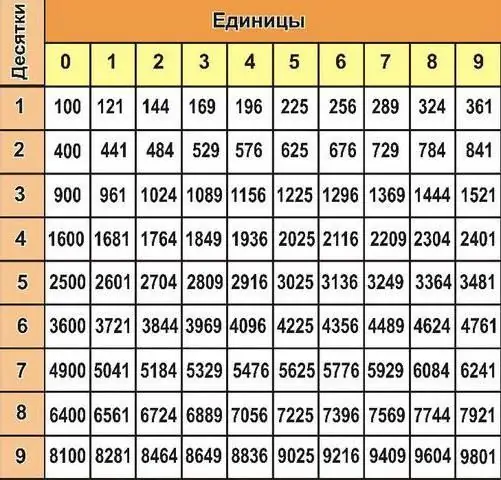
As you can see, some exponents can be guessed intuitively if you have a technical mindset and knowledge of the multiplication table. However, larger values will require a power table. It can be used even by those who do not understand anything at all in complex mathematical topics. The left column contains numbers (base a), the top row of numbers is the value of the power c, to which the number a is raised. At the intersection, the cells define the values of the numbers that are the answer (ac=b). Let's take, for example, the very first cell with the number 10 and square it, we get the value 100, which is indicated at the intersection of our two cells. Everything is so simple and easy that even the most real humanist will understand!
Equations and inequalities
It turns out that whenUnder certain conditions, the exponent is the logarithm. Therefore, any mathematical numerical expressions can be written as a logarithmic equation. For example, 34=81 can be written as the logarithm of 81 to base 3, which is four (log381=4). For negative degrees, the rules are the same: 2-5=1/32 written as a logarithm, we get log2 (1/32)=-5. One of the most fascinating sections of mathematics is the topic of "logarithms". We will consider examples and solutions of equations a little lower, immediately after studying their properties. For now, let's look at what inequalities look like and how to distinguish them from equations.

The following expression is given: log2(x-1) > 3 - it is a logarithmic inequality, since the unknown value "x" is under the sign of the logarithm. The expression also compares two quantities: the base two logarithm of the desired number is greater than the number three.
The most important difference between logarithmic equations and inequalities is that equations with logarithms (example - logarithm2x=√9) imply in the answer one or more specific numerical values, while when solving an inequality, both the range of acceptable values and the breakpoints of this function are determined. As a result, the answer is not a simple set of individual numbers, as in the answer of the equation, but a continuous series or set of numbers.

Basic theorems on logarithms
When solving primitive tasks to find the values of the logarithm, you may not know its properties. However, when it comes to logarithmic equations or inequalities, first of all, it is necessary to clearly understand and apply in practice all the basic properties of logarithms. We will get acquainted with the examples of equations later, let's first analyze each property in more detail.
- The basic identity looks like this: alogaB=B. It only applies if a is greater than 0, not equal to one, and B is greater than zero.
- The logarithm of the product can be represented in the following formula: logd(s1s2)=logds1 + logds2. In this case, the obligatory condition is: d, s1 and s2 > 0; a≠1. You can give a proof for this formula of logarithms, with examples and a solution. Let logas1 =f1 and logas 2=f2, then af1=s1, a f2=s2. We get that s1s2 =af1a f2=af1+f2 (degree properties), and further by definition: loga(s1 s2)=f1+ f2=log as1 + logas2, which was to be proved.
- The logarithm of the quotient looks like this: loga(s1/s2)=log as1- logas2.
- The theorem in the form of a formula takes the following form: logaqbn =n/q logab.
This formula is called the "property of the degree of the logarithm". It resembles the properties of ordinary degrees, and it is not surprising, because all mathematics rests on regular postulates. Let's look at the proof.
Let logab=t, we get at=b. If you raise both sides to the m power: atn=b;
but because atn=(aq)nt/q=b, hence logaq bn=(nt)/t, then logaq bn =n/q logab. Theorem proven.
Examples of problems and inequalities
The most common types of logarithm problems are examples of equations and inequalities. They are found in almost all problem books, and are also included in the mandatory part of exams in mathematics. To enter a university or pass entrance tests in mathematics, you need to know how to solve such problems correctly.
Unfortunately, there is no single plan or scheme for solving and determining the unknown value of the logarithm, but certain rules can be applied to each mathematical inequality or logarithmic equation. First of all, you should find out whether the expression can be simplified or reduced to a general form. You can simplify long logarithmic expressions if you use their properties correctly. Let's get to know them soon.
When solving logarithmic equations,it is necessary to determine what kind of logarithm we have before us: an example of an expression may contain a natural logarithm or a decimal one.
Here are examples of decimal logarithms: ln100, ln1026. Their solution boils down to the fact that you need to determine the degree to which the base 10 will be equal to 100 and 1026, respectively. For solutions of natural logarithms, one must apply logarithmic identities or their properties. Let's look at examples of solving logarithmic problems of various types.
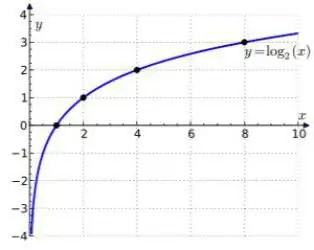
How to use logarithm formulas: with examples and solutions
So, let's look at examples of using the main theorems about logarithms.
- The property of the logarithm of the product can be used in tasks where it is necessary to decompose a large value of the number b into simpler factors. For example, log24 + log2128=log2(4128)=log 2512. The answer is 9.
- log48=log22 23 =3/2 log22=1, 5 - as you can see, by applying the fourth property of the degree of the logarithm, we managed to solve at first glance a complex and unsolvable expression. All you have to do is factor the base and then take the power out of the sign of the logarithm.

Assignments from the exam
Logarithms are often found in entrance exams, especially a lot of logarithmic problems in the Unified State Examination (state exam for all school graduates). Usually these tasks are present not only in part A (the mosteasy test part of the exam), but also in part C (the most difficult and voluminous tasks). The exam requires an accurate and perfect knowledge of the topic "Natural logarithms".
Examples and problem solutions are taken from the official versions of the exam. Let's see how such tasks are solved.
Given log2(2x-1)=4. Solution:
rewrite the expression, simplifying it a bit log2 (2x-1)=22, by the definition of the logarithm we get that 2x-1=24, hence 2x=17; x=8, 5.
Following a few guidelines, following which you can easily solve all equations containing expressions that are under the sign of the logarithm.
- It is best to reduce all logarithms to the same base so that the solution is not cumbersome and confusing.
- All expressions under the logarithm sign are indicated as positive, so when multiplying the exponent of the expression that is under the logarithm sign and as its base, the expression remaining under the logarithm must be positive.






