What is the angle bisector of a triangle? To this question, a well-known saying breaks out of the tongue of some people: "This is a rat running around the corners and dividing the corner in half." If the answer is supposed to be "with humor", then perhaps it is correct. But from a scientific point of view, the answer to this question should have sounded something like this: "This is a ray starting at the top of the corner and dividing the latter into two equal parts." In geometry, this figure is also perceived as a segment of the bisector until it intersects with the opposite side of the triangle. This is not an erroneous opinion. What else is known about the angle bisector, besides its definition?
Like any locus of points, it has its own characteristics. The first of them is rather not even a sign, but a theorem that can be briefly expressed as follows: "If the bisector divides the opposite side into two parts, then their ratio will correspond to the ratio of the sides of the largetriangle".
The second property it has: the intersection point of the bisectors of all angles is called the incenter.
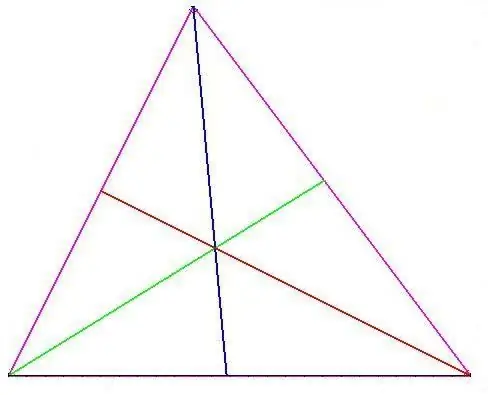
Third sign: the bisectors of one internal and two external angles of a triangle intersect at the center of one of the three inscribed circles in it.
The fourth property of the angle bisector of a triangle is that if each of them is equal, then the last one is isosceles.
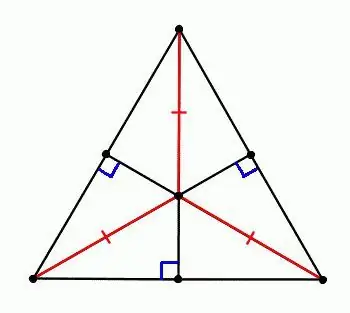
The fifth sign also concerns an isosceles triangle and is the main guideline for its recognition in the drawing by bisectors, namely: in an isosceles triangle, it simultaneously acts as a median and height.
The bisector of an angle can be constructed using a compass and straightedge:
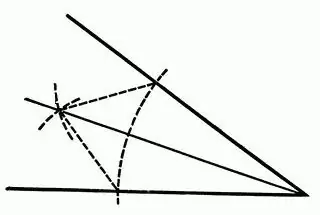
The sixth rule says that it is impossible to construct a triangle using the latter only with the available bisectors, just as it is impossible to construct a doubling of a cube, a square of a circle and a trisection of an angle in this way. Strictly speaking, this is all the properties of the angle bisector of a triangle.
If you carefully read the previous paragraph, then perhaps you are interested in one phrase. "What is the trisection of an angle?" - you will surely ask. The trisectrix is a bit similar to the bisector, but if you draw the latter, then the angle will be divided into two equal parts, and when constructing a trisection, intothree. Naturally, the bisector of an angle is easier to remember, because the trisection is not taught at school. But for the sake of completeness, I’ll tell you about her.
A trisector, as I said, cannot be built only with a compass and a ruler, but it can be created using Fujita's rules and some curves: Pascal's snails, quadratrices, Nicomedes' conchoids, conic sections, Archimedes' spirals.
Problems on the trisection of an angle are quite simply solved using nevsis.
In geometry there is a theorem about angle trisectors. It is called the Morley (Morley) theorem. She states that the points of intersection of the trisectors in the middle of each angle will be the vertices of an equilateral triangle.
A small black triangle inside a large one will always be equilateral. This theorem was discovered by British scientist Frank Morley in 1904.

Here's all there is to learn about splitting an angle: the trisector and bisector of an angle always require detailed explanations. But here many definitions that have not yet been disclosed by me were given: Pascal's snail, Nicomedes' conchoid, etc. Make no mistake, more can be written about them.






