The study of the processes occurring in statistical systems is complicated by the minimum size of particles and their huge number. It is practically impossible to consider each particle separately, therefore, statistical quantities are introduced: the average speed of particles, their concentration, particle mass. The formula that characterizes the state of the system, taking into account microscopic parameters, is called the basic equation of the molecular-kinetic theory of gases (MKT).
A little bit about the average particle speed
Determination of the particle velocity was first carried out experimentally. A well-known experiment from the school curriculum, conducted by Otto Stern, made it possible to create an idea of particle velocities. During the experiment, the motion of silver atoms in rotating cylinders was studied: first, in a stationary state of the installation, then when it rotated with a certain angular velocity.
As a result, it was found that the speed of silver molecules exceeds the speed of sound and is 500 m/s. The fact is quite interesting, since it is difficult for a person to feel such speeds of movement of particles in substances.
Ideal gas
Continue researchIt seems possible only in a system whose parameters can be determined by direct measurements using physical instruments. Speed is measured with a speedometer, but the idea of attaching a speedometer to a single particle is absurd. Only a macroscopic parameter associated with particle motion can be measured directly.

Consider gas pressure. The pressure on the walls of the vessel is created by the impacts of the molecules of the gas in the vessel. The peculiarity of the gaseous state of matter is in sufficiently large distances between the particles and their small interaction with each other. This allows you to directly measure its pressure.
Any system of interacting bodies is characterized by potential energy and kinetic energy of motion. Real gas is a complex system. The variability of potential energy does not lend itself to systematization. The problem can be solved by introducing a model that carries the characteristic properties of the gas, sweeping aside the complexity of the interaction.
Ideal gas is a state of matter in which the interaction of particles is negligible, the potential energy of interaction tends to zero. Only the energy of motion, which depends on the speed of particles, can be considered significant.

Ideal gas pressure
To reveal the relationship between the pressure of a gas and the speed of movement of its particles allows the basic equation of the MKT of an ideal gas. A particle moving in a vessel, upon impact with the wall, transfers to it an impulse, the value of which can be determined on the basis of the second lawNewton:
F∆t=2m0vx
Change in the momentum of a particle during elastic impact is associated with a change in the horizontal component of its velocity. F is the force acting from the side of the particle on the wall for a short time t; m0 - particle mass.
All gas particles collide with the surface of area S during the time ∆t, moving in the direction of the surface with speed vx and located in a cylinder of volume Sυx Δt. At particle concentration n, exactly half of the molecules move towards the wall, the other half move in the opposite direction.
Having considered the collision of all particles, we can write Newton's law for the force acting on the area:
F∆t=nm0vx2S∆t
Since gas pressure is defined as the ratio of the force acting perpendicular to the surface to the area of the latter, we can write:
p=F: S=nm0vx2
The resulting relation as the basic equation of the MKT cannot describe the entire system, since only one direction of motion is considered.
Maxwell distribution
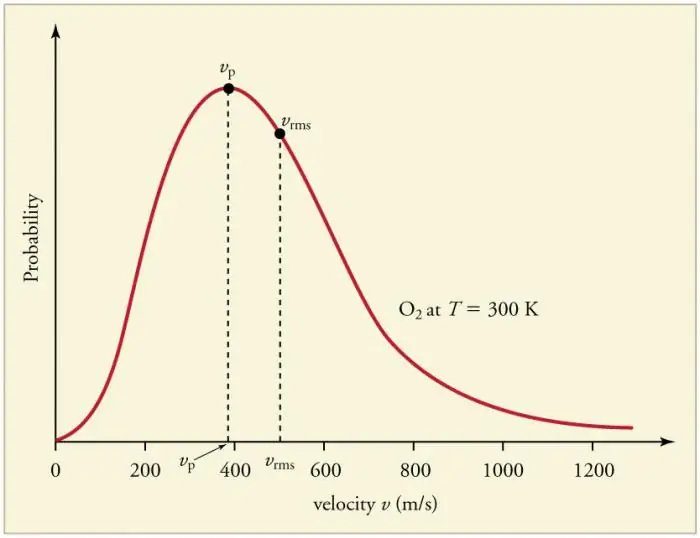
Continuous frequent collisions of gas particles with the walls and with each other lead to the establishment of a certain statistical distribution of particles in terms of velocities (energies). The directions of all velocity vectors turn out to be equally probable. This distribution is called the Maxwell distribution. In 1860 this pattern wasderived by J. Maxwell on the basis of the MKT. The main parameters of the distribution law are called velocities: probable, corresponding to the maximum value of the curve, and root-mean-square vkv=√‹v2› - the mean square of the particle velocity.
Increase in gas temperature corresponds to increase in velocity.
Based on the fact that all speeds are equal, and their modules have the same value, we can assume:
‹v2›=‹vx2› + ‹v y2› + ‹vz2›, from: ‹ vx2›=‹v2›: 3
The basic equation of the MKT, taking into account the average value of the gas pressure, is:
p=nm0‹v2›: 3.
This relationship is unique in that it determines the relationship between microscopic parameters: speed, particle mass, particle concentration and gas pressure in general.
Using the concept of the kinetic energy of particles, the basic equation of the MKT can be rewritten differently:
p=2nm0‹v2›: 6=2n‹Ek›: 3
The pressure of a gas is proportional to the average value of the kinetic energy of its particles.
Temperature
Interestingly, for a constant amount of gas in a closed vessel, one can relate the gas pressure and the average value of the particle motion energy. In this case, pressure can be measured by measuring the energyparticles.
What to do? What value can be compared with kinetic energy? Temperature turns out to be such a value.

Temperature is a measure of the thermal state of substances. To measure it, a thermometer is used, the basis of which is the thermal expansion of the working fluid (alcohol, mercury) when heated. The thermometer scale is created experimentally. Usually, marks are placed on it corresponding to the position of the working fluid during some physical process occurring at a constant thermal state (boiling water, melting ice). Different thermometers have different scales. For example, Celsius, Fahrenheit.

Universal temperature scale
Gas thermometers can be considered more interesting in terms of independence from the properties of the working fluid. Their scale does not depend on the type of gas used. In such a device, one can hypothetically single out the temperature at which the gas pressure tends to zero. Calculations show that this value corresponds to -273.15 oC. The temperature scale (absolute temperature scale or Kelvin scale) was introduced in 1848. The possible temperature of zero gas pressure was taken as the main point of this scale. A unit segment of the scale is equal to a unit value of the Celsius scale. It seems more convenient to write down the basic MKT equation using temperature when studying gas processes.
Relationship between pressure and temperature
Empirically, you can verify thatproportionality of gas pressure to its temperature. At the same time, it was found that the pressure is directly proportional to the concentration of particles:
P=nkT,
where T is absolute temperature, k is a constant equal to 1.38•10-23J/K.
The fundamental value, which has a constant value for all gases, is called the Boltzmann constant.
Comparing the dependence of pressure on temperature and the basic equation of the MKT gases, we can write:
‹Ek›=3kT: 2
The average value of the kinetic energy of the movement of gas molecules is proportional to its temperature. That is, temperature can serve as a measure of the kinetic energy of particle motion.






