One of the figures that occurs when solving geometric problems in space is a cone. It, unlike polyhedra, belongs to the class of figures of rotation. Let's consider in the article what is meant by it in geometry, and explore the characteristics of various sections of the cone.
Cone in geometry
Assume that there is some curve on the plane. It can be a parabola, a circle, an ellipse, and so on. Take a point that does not belong to the specified plane, and connect all points of the curve to it. The resulting surface is called a cone or simply a cone.
If the original curve is closed, then the conical surface can be filled with matter. The figure obtained in this way is a three-dimensional body. It is also called a cone. Several paper cones are shown below.

The conical surface is found in everyday life. For example, an ice cream cone or a striped traffic cone has this shape, which is designed to attract the attention of drivers andpedestrians.

Types of cones
As you might guess, the figures under consideration differ from each other by the type of curve on which they are formed. For example, there is a round cone or an elliptical one. This curve is called the base of the figure. However, the shape of the base is not the only feature that allows the classification of cones.
The second important characteristic is the position of the height relative to the base. The height of a cone is a straight line segment, which is lowered from the top of the figure to the plane of the base and is perpendicular to this plane. If the height intersects the base in the geometric center (for example, in the center of the circle), then the cone will be straight, if the perpendicular segment falls to any other point of the base or beyond it, then the figure will be oblique.
Further in the article we will consider only a round straight cone as a bright representative of the considered class of figures.
Geometric names of cone elements
It was said above that the cone has a base. It is bounded by a circle, which is called the guide of the cone. The segments connecting the guide to a point that does not lie in the plane of the base are called generators. The set of all points of the generators is called the conical or lateral surface of the figure. For a round right cone, all generators have the same length.
The point where the generators intersect is called the top of the figure. Unlike polyhedra, a cone has a single vertex and noedge.
A straight line passing through the top of the figure and the center of the circle is called the axis. The axis contains the height of a straight cone, so it forms a right angle with the plane of the base. This information is important when calculating the area of the axial section of the cone.
Round straight cone - rotation figure
The considered cone is a fairly symmetrical figure, which can be obtained as a result of the rotation of the triangle. Suppose we have a triangle with a right angle. To get a cone, it is enough to rotate this triangle around one of the legs as shown in the figure below.
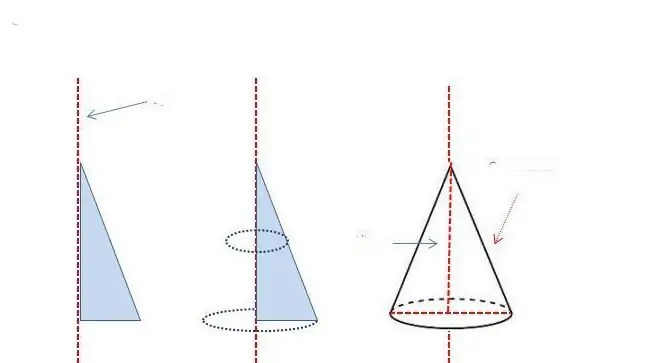
It can be seen that the axis of rotation is the axis of the cone. One of the legs will be equal to the height of the figure, and the second leg will become the radius of the base. The hypotenuse of a triangle as a result of rotation will describe a conical surface. It will be the generatrix of the cone.
This method of obtaining a round straight cone is convenient to use to study the mathematical relationship between the linear parameters of the figure: the height h, the radius of the round base r and the guide g. The corresponding formula follows from the properties of a right triangle. It is listed below:
g2=h2+ r2.
Since we have one equation and three variables, this means that to uniquely set the parameters of a round cone, you need to know any two quantities.
Sections of a cone by a plane that does not contain the vertex of the figure
The question of constructing sections of a figure is nottrivial. The fact is that the shape of the section of the cone by the surface depends on the relative position of the figure and the secant.
Assume that we intersect the cone with a plane. What will be the result of this geometric operation? Section shape options are shown in the figure below.
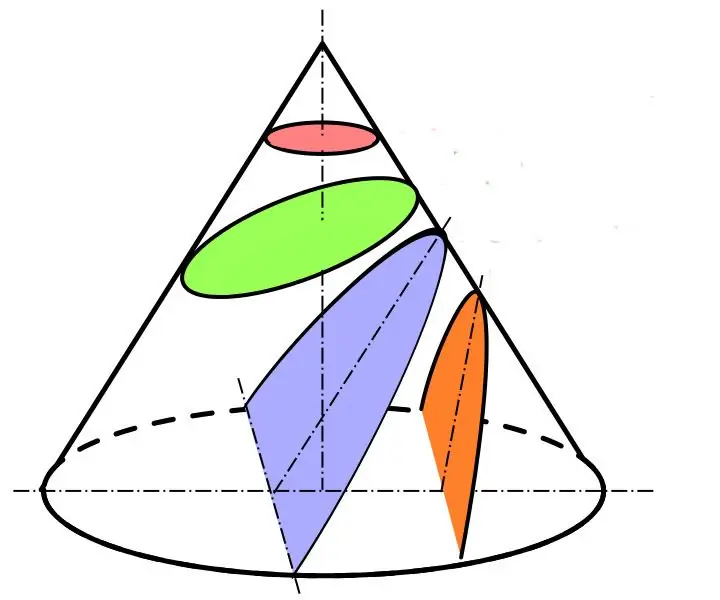
The pink section is a circle. It is formed as a result of the intersection of the figure with a plane that is parallel to the base of the cone. These are sections perpendicular to the axis of the figure. The figure formed above the cutting plane is a cone, similar to the original one, but having a smaller circle at the base.
The green section is an ellipse. It is obtained if the cutting plane is not parallel to the base, but it only intersects the lateral surface of the cone. A figure cut off above the plane is called an elliptical oblique cone.
The blue and orange sections are parabolic and hyperbolic, respectively. As can be seen from the figure, they are obtained if the cutting plane simultaneously intersects the side surface and the base of the figure.
To determine the areas of the sections of the cone that were considered, it is necessary to use the formulas for the corresponding figure on the plane. For example, for a circle, this is the number Pi multiplied by the square of the radius, and for an ellipse, this is the product of Pi and the length of the minor and major semiaxes:
circle: S=pir2;
ellipse: S=piab.
Sections containing the top of the cone
Now consider the options for sections that arise if the cutting plane ispass through the top of the cone. Three cases are possible:
- The section is a single point. For example, a plane passing through the vertex and parallel to the base gives just such a section.
- The section is a straight line. This situation occurs when the plane is tangent to a conical surface. The straight line of the section in this case will be the generatrix of the cone.
- Axial section. It is formed when the plane contains not only the top of the figure, but also its entire axis. In this case, the plane will be perpendicular to the round base and will divide the cone into two equal parts.
Obviously, the areas of the first two types of sections are equal to zero. As for the sectional area of the cone for the 3rd type, this issue is discussed in more detail in the next paragraph.
Axial section
It was noted above that the axial section of a cone is the figure formed when the cone is intersected by a plane passing through its axis. It is easy to guess that this section will represent the figure shown in the figure below.

This is an isosceles triangle. The vertex of the axial section of the cone is the vertex of this triangle, formed by the intersection of identical sides. The latter are equal to the length of the generatrix of the cone. The base of the triangle is the diameter of the base of the cone.
Calculating the area of the axial section of a cone is reduced to finding the area of the resulting triangle. If the radius of the base r and the height h of the cone are initially known, then the area S of the section under consideration will be:
S=hr.
Thisthe expression is a consequence of applying the standard formula for the area of a triangle (half the product of the height times the base).
Note that if the generatrix of a cone is equal to the diameter of its round base, then the axial section of the cone is an equilateral triangle.
A triangular section is formed when the cutting plane is perpendicular to the base of the cone and passes through its axis. Any other plane parallel to the named one will give a hyperbola in section. However, if the plane contains the vertex of the cone and intersects its base not through the diameter, then the resulting section will also be an isosceles triangle.
The problem of determining the linear parameters of the cone
Let's show how to use the formula written for the area of the axial section to solve a geometric problem.
It is known that the area of the axial section of the cone is 100 cm2. The resulting triangle is equilateral. What is the height of the cone and the radius of its base?
Since the triangle is equilateral, its height h is related to the length of side a as follows:
h=√3/2a.
Given that the side of the triangle is twice the radius of the base of the cone, and substituting this expression into the formula for the cross-sectional area, we get:
S=hr=√3/22rr=>
r=√(S/√3).
Then the height of the cone is:
h=√3/22r=√3√(S/√3)=√(√3S).
It remains to substitute the value of the area from the condition of the problemand get the answer:
r=√(100/√3) ≈ 7.60 cm;
h=√(√3100) ≈ 13, 16 cm.
In what areas is it important to know the parameters of the considered sections?
The study of various types of cone sections is not only of theoretical interest, but also has practical applications.
First, it should be noted the area of aerodynamics, where with the help of conic sections it is possible to create ideal smooth shapes of solid bodies.
Secondly, conic sections are trajectories along which space objects move in gravitational fields. What specific type of section represents the trajectory of the system's cosmic bodies is determined by the ratio of their masses, absolute velocities and distances between them.






