The natural phenomena and processes around us are quite complex. For their exact physical description, a cumbersome mathematical apparatus should be used and a large number of significant factors should be taken into account. To avoid this problem, some simplified models are used in physics, which greatly facilitate the mathematical analysis of the process, but practically do not affect the accuracy of its description. One of them is the ideal gas model. Let's consider it in more detail in the article.
The concept of an ideal gas
An ideal gas is a state of aggregation of a substance, which consists of material points that do not interact with each other. Let us explain this definition in more detail.
Firstly, we are talking about material points as objects that make up an ideal gas. This means that its molecules and atoms do not have a size, but have a certain mass. It's boldan approximation can be made taking into account the fact that in all real gases at low pressures and high temperatures, the distance between molecules is much greater than their linear dimensions.
Secondly, the molecules in an ideal gas should not interact with each other. In reality, such interactions always exist. So, even atoms of noble gases experience dipole-dipole attraction. In other words, van der Waals interactions are present. However, compared with the kinetic energy of rotation and translational movement of molecules, these interactions are so small that they do not affect the properties of gases. Therefore, they can not be considered when solving practical problems.
It is important to note that not all gases in which the density is low and the temperature is high can be considered ideal. In addition to van der Waals interactions, there are other, stronger types of bonds, for example, hydrogen bonds between H2O molecules, which lead to a gross violation of the gas ideality conditions. For this reason, water vapor is not an ideal gas, but air is.

Physical model of an ideal gas
This model can be represented as follows: suppose that the gas system contains N particles. These can be atoms and molecules of various chemicals and elements. The number of N particles is large, so the unit "mole" is usually used to describe it (1 mole corresponds to Avogadro's number). They all move in some volume V. Particle motionsare chaotic and independent of each other. Each of them has a certain speed v and moves along a straight path.
Theoretically, the probability of collision between particles is almost zero, since their size is small compared to the interparticle distances. However, if such a collision occurs, then it is absolutely elastic. In the latter case, the total momentum of the particles and their kinetic energy are conserved.
The considered model of ideal gases is a classical system with a huge number of elements. Therefore, the speed and energy of particles in it obey the statistical distribution of Maxwell-Boltzmann. Some particles have low velocities, while others have high velocities. In this case, there is a certain narrow limit of velocities, in which the most probable values of this quantity lie. The velocity distribution of nitrogen molecules is shown schematically below.
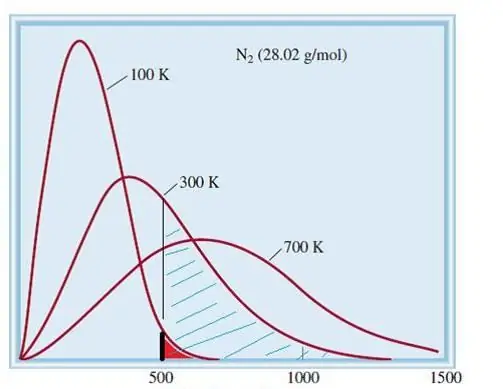
Kinetic theory of gases
The model of ideal gases described above uniquely determines the properties of gases. This model was first proposed by Daniel Bernoulli in 1738.

Subsequently it was developed to its current state by August Kroenig, Rudolf Clausius, Mikhail Lomonosov, James Maxwell, Ludwig Boltzmann, Marian Smoluchowski and other scientists.
The kinetic theory of fluid substances, on the basis of which the ideal gas model is built, explains two important macroscopic properties of the system based on its microscopic behavior:
- The pressure in gases is the result of the collision of particles with the walls of the vessel.
- The temperature in the system is the result of the manifestation of the constant movement of molecules and atoms.
Let's expand on both conclusions of the kinetic theory.
Gas pressure
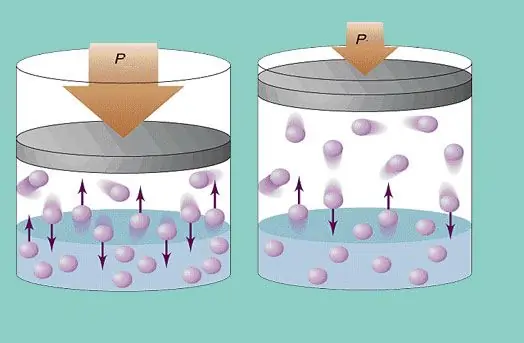
The ideal gas model assumes a constant chaotic movement of particles in the system and their constant collision with the walls of the vessel. Each such collision is considered absolutely elastic. The particle mass is small (≈10-27-10-25 kg). Therefore, it cannot create a lot of pressure in a collision. Nevertheless, the number of particles, and hence the number of collisions, is huge (≈1023). In addition, the root mean square velocity of the elements is several hundred meters per second at room temperature. All this leads to the creation of appreciable pressure on the walls of the vessel. It can be calculated using the following formula:
P=Nmvcp2 / (3V), where vcp is root mean square velocity, m is particle mass.
Absolute temperature
According to the ideal gas model, the temperature is uniquely determined by the average kinetic energy of a molecule or atom in the system under study. You can write the following expression that relates kinetic energy and absolute temperature for an ideal gas:
mvcp2 / 2=3 / 2kB T.
Here kB is the Boltzmann constant. From this equality we get:
T=m vcp2 / (3kB).
Universal equation of state
If we combine the above expressions for absolute pressure P and absolute temperature T, we can write the following equality:
PV=nRT.
Here n is the amount of substance in moles, R is the gas constant introduced by D. I. Mendeleev. This expression is the most important equation in the theory of ideal gases, because it combines three thermodynamic parameters (V, P, T) and does not depend on the chemical characteristics of the gas system.

The universal equation was first experimentally derived by the French physicist Emile Clapeyron in the 19th century and then brought to its modern form by the Russian chemist Mendeleev, which is why it currently bears the names of these scientists.






