Quantitative study of the dynamics and kinematics of rotational motion requires knowledge of the moment of inertia of a material point and a rigid body relative to the axis of rotation. We will consider in the article what parameter we are talking about, and also give a formula for determining it.
General information about the physical quantity
First, let's define the moment of inertia of a material point and a rigid body, and then show how it should be used in solving practical problems.
Under the specified physical characteristic for a point with a mass m, which rotates around the axis at a distance r, the following value is meant:
I=mr².
Where it follows that the unit of measurement of the studied parameter is kilograms per square meter (kgm²).
If, instead of a point around an axis, a body of complex shape rotates, which has an arbitrary distribution of mass inside itself, then its moment of inertia is determinedso:
I=∫m(r²dm)=ρ∫V(r²dV).
Where ρ is the density of the body. Using the integral formula, you can determine the value of I for absolutely any system of rotation.
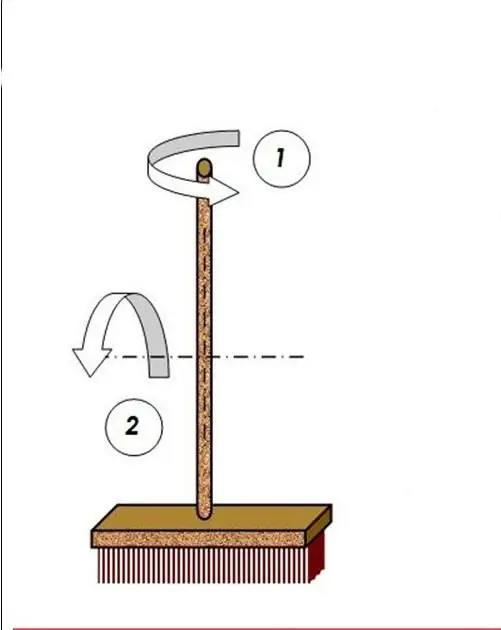
Moment of inertia has exactly the same meaning for rotation as mass has for translational motion. For example, everyone knows that it is easiest to rotate a floor mop around an axis passing through its handle than through a perpendicular one. This is due to the fact that the moment of inertia in the first case is much less than in the second.
I value for bodies of different shapes
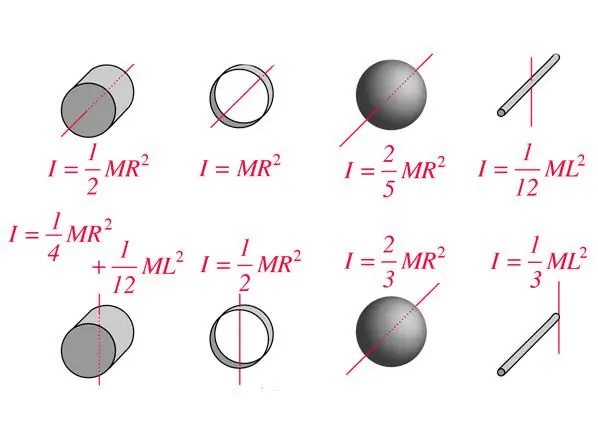
When solving problems in physics for rotation, it is often necessary to know the moment of inertia for a body of a specific geometric shape, for example, for a cylinder, ball or rod. If we apply the formula written above for I, then it is easy to obtain the corresponding expression for all marked bodies. Below are the formulas for some of them:
rod: I=1 / 12ML²;
cylinder: I=1 / 2MR²;
sphere: I=2 / 5MR².
Here I are given for the axis of rotation, which passes through the center of mass of the body. In the case of a cylinder, the axis is parallel to the generator of the figure. The moment of inertia for other geometric bodies and options for the location of the axes of rotation can be found in the corresponding tables. Note that to determine I different figures, it is enough to know only one geometric parameter and the mass of the body.
Steiner's theorem and formula

Moment of inertia can be determined if the axis of rotation is located at some distance from the body. To do this, you should know the length of this segment and the value IOof the body relative to the axis passing through the center of its mass, which should be parallel to the one under consideration. Establishing a connection between the parameter IO and the unknown value I is fixed in Steiner's theorem. The moment of inertia of a material point and a rigid body is mathematically written as follows:
I=IO+ Mh2.
Here M is the mass of the body, h is the distance from the center of mass to the axis of rotation, relative to which it is necessary to calculate I. This expression is easy to obtain on your own if you use the integral formula for I and take into account that all points of the body are at distances r=r0 + h.
Steiner's theorem greatly simplifies the definition of I for many practical situations. For example, if you need to find I for a rod of length L and mass M with respect to an axis that passes through its end, then applying the Steiner theorem allows you to write:
I=IO+ M(L / 2)2=1 / 12ML 2+ ML2 / 4=ML2 / 3.
You can refer to the corresponding table and see that it contains exactly this formula for a thin rod with an axis of rotation at its end.
Moment equation
In the physics of rotation there is a formula called the equation of moments. It looks like this:
M=Iα.
Here M is the moment of force, α is the angular acceleration. As you can see, the moment of inertia of a material point and a rigid body and the moment of force are linearly related to each other. The value M determines the possibility of some force F to create a rotational motion with acceleration α in the system. To calculate M, use the following simple expression:
M=Fd.
Where d is the shoulder of the moment, which is equal to the distance from the force vector F to the axis of rotation. The smaller the arm d, the less ability the force will have to create rotation of the system.
The equation of moments in its meaning is fully consistent with Newton's second law. In this case, I plays the role of the inertial mass.
Example of problem solving

Let's imagine a system that is a cylinder fixed on a vertical axis with a weightless horizontal rod. It is known that the axis of rotation and the main axis of the cylinder are parallel to each other, and the distance between them is 30 cm. The mass of the cylinder is 1 kg, and its radius is 5 cm. A force of 10 N tangent to the trajectory of rotation acts on the figure, the vector of which passes through main axis of the cylinder. It is necessary to determine the angular acceleration of the figure, which this force will cause.
First, let's calculate the moment of inertia of the I cylinder. To do this, apply the Steiner theorem, we have:
I=IO+ M d²=1 / 2MR² + Md²=1 / 210.05² + 10, 3²=0.09125 kgm².
Before using the moment equation, you need todetermine the moment of force M. In this case, we have:
M=Fd=100, 3=3 Nm.
Now you can determine the acceleration:
α=M/I=3/0.09125 ≈ 32.9 rad/s².
The calculated angular acceleration indicates that every second the speed of the cylinder will increase by 5.2 revolutions per second.






