In the mathematical description of rotational motion, it is important to know the moment of inertia of the system about the axis. In the general case, the procedure for finding this quantity involves the implementation of the integration process. The so-called Steiner theorem makes it easier to calculate. Let's consider it in more detail in the article.
What is moment of inertia?
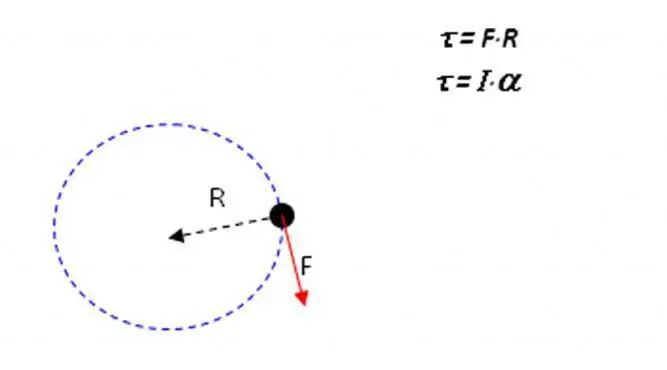
Before giving the formulation of Steiner's theorem, it is necessary to deal with the very concept of the moment of inertia. Suppose there is some body of a certain mass and arbitrary shape. This body can be either a material point or any two-dimensional or three-dimensional object (rod, cylinder, ball, etc.). If the object in question makes a circular motion around some axis with constant angular acceleration α, then the following equation can be written:
M=Iα
Here, the value M represents the total moment of forces, which gives acceleration α to the entire system. The coefficient of proportionality between them - I, is calledmoment of inertia. This physical quantity is calculated using the following general formula:
I=∫m (r2dm)
Here r is the distance between the element with mass dm and the rotation axis. This expression means that it is necessary to find the sum of the products of the squared distances r2 and the elementary mass dm. That is, the moment of inertia is not a pure characteristic of the body, which distinguishes it from linear inertia. It depends on the distribution of mass throughout the object that rotates, as well as on the distance to the axis and on the orientation of the body relative to it. For example, a rod will have a different I if it is rotated about the center of mass and about the end.
Moment of inertia and Steiner's theorem

The famous Swiss mathematician, Jakob Steiner, proved the theorem on parallel axes and the moment of inertia, which now bears his name. This theorem postulates that the moment of inertia for absolutely any rigid body of arbitrary geometry relative to some axis of rotation is equal to the sum of the moment of inertia about the axis that intersects the center of mass of the body and is parallel to the first, and the product of the body mass times the square of the distance between these axes. Mathematically, this formulation is written as follows:
IZ=IO + ml2
IZ and IO - moments of inertia about the Z-axis and the O-axis parallel to it, which passes through the center of mass of the body, l - distance between lines Z and O.
The theorem allows, knowing the value of IO, to calculateany other moment IZ about an axis that is parallel to O.
Proof of the theorem
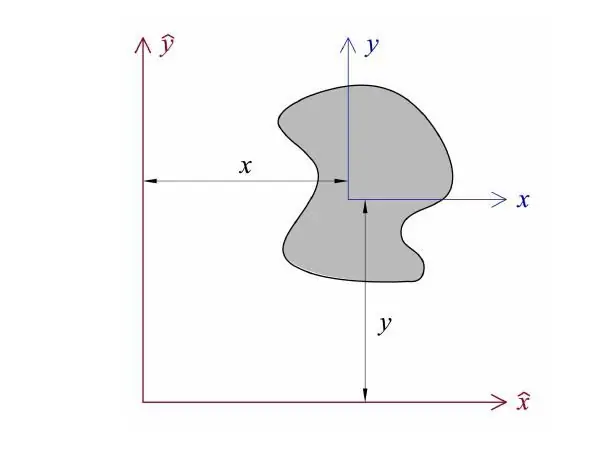
The Steiner theorem formula can be easily obtained by yourself. To do this, consider an arbitrary body on the xy plane. Let the origin of coordinates pass through the center of mass of this body. Let's calculate the moment of inertia IO which passes through the origin perpendicular to the xy plane. Since the distance to any point of the body is expressed by the formula r=√ (x2 + y2), then we get the integral:
IO=∫m (r2dm)=∫ m ((x2+y2) dm)
Now let's move the axis parallel along the x-axis by a distance l, for example, in the positive direction, then the calculation for the new axis of the moment of inertia will look like this:
IZ=∫m(((x+l)2+y 2)dm)
Expand the full square in brackets and divide the integrands, we get:
IZ=∫m ((x2+l 2+2xl+y2)dm)=∫m ((x2 +y2)dm) + 2l∫m (xdm) + l 2∫mdm
The first of these terms is the value IO, the third term, after integration, gives the term l2m, and here the second term is zero. The zeroing of the specified integral is due to the fact that it is taken from the product of x and mass elements dm, which inaverage gives zero, since the center of mass is at the origin. As a result, the formula of the Steiner theorem is obtained.
The considered case on the plane can be generalized to a three-dimensional body.
Checking the Steiner formula on the example of a rod
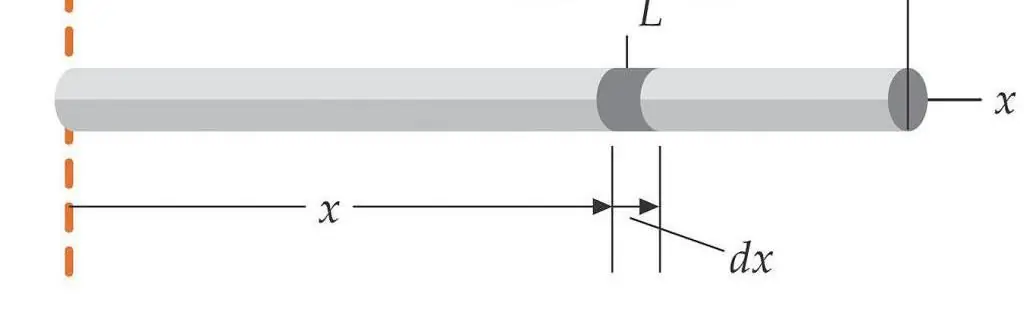
Let's give a simple example to demonstrate how to use the above theorem.
It is known that for a rod of length L and mass m, the moment of inertia IO(the axis passes through the center of mass) is equal to mL2 /12, and the moment IZ(the axis passes through the end of the rod) is equal to mL2/3. Let's check this data using Steiner's theorem. Since the distance between the two axles is L/2, then we get the moment IZ:
IZ=IO+ m(L/2)2=mL2/12 + mL2/4=4mL2 /12=mL2/3
That is, we checked the Steiner formula and got the same value for IZ as in the source.
Similar calculations can be carried out for other bodies (cylinder, ball, disk), while obtaining the necessary moments of inertia, and without performing integration.
Moment of inertia and perpendicular axes
The considered theorem concerns parallel axes. For completeness of information, it is also useful to give a theorem for perpendicular axes. It is formulated as follows: for a flat object of arbitrary shape, the moment of inertia about an axis perpendicular to it will be equal to the sum of two moments of inertia about two mutually perpendicular and lyingin the plane of the axes object, with all three axes passing through the same point. Mathematically, this is written as follows:
Iz=Ix + Iy
Here z, x, y are three mutually perpendicular axes of rotation.
The essential difference of this theorem from Steiner's theorem is that it is applicable only to flat (two-dimensional) solid objects. Nevertheless, in practice it is widely used, mentally cutting the body into separate layers, and then adding the obtained moments of inertia.






