When solving problems of moving objects, in some cases their spatial dimensions are neglected, introducing the concept of a material point. For another type of problems, in which bodies at rest or rotating bodies are considered, it is important to know their parameters and the points of application of external forces. In this case, we are talking about the moment of forces about the axis of rotation. We will consider this issue in the article.
The concept of moment of force
Before giving the formula for the moment of force relative to the fixed axis of rotation, it is necessary to clarify what phenomenon will be discussed. The figure below shows a wrench of length d, a force F is applied to its end. It is easy to imagine that the result of its action will be the rotation of the wrench counterclockwise and unscrewing the nut.
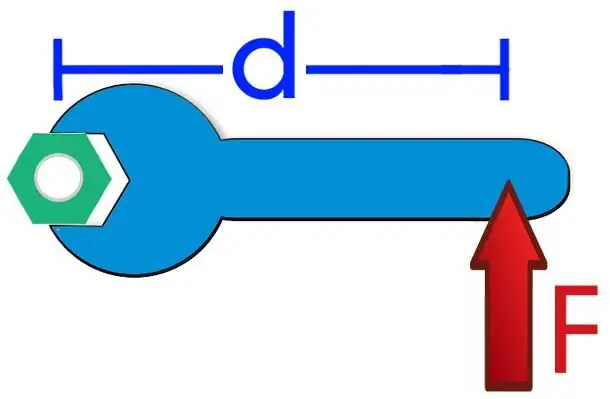
According to the definition, the moment of force about the axis of rotation isthe product of the shoulder (d in this case) and the force (F), that is, the following expression can be written: M=dF. It should immediately be noted that the above formula is written in scalar form, that is, it allows you to calculate the absolute value of the moment M. As can be seen from the formula, the unit of measurement of the considered quantity is newtons per meter (Nm).
Moment of force is a vector quantity
As mentioned above, the moment M is actually a vector. To clarify this statement, consider another figure.
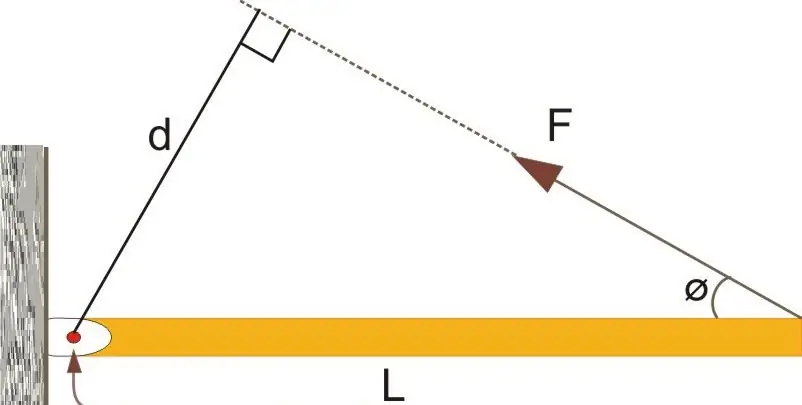
Here we see a lever of length L, which is fixed on the axis (shown by the arrow). A force F is applied to its end at an angle Φ. It is not difficult to imagine that this force will cause the lever to rise. The formula for the moment in vector form in this case will be written as follows: M¯=L¯F¯, here the line over the symbol means that the quantity in question is a vector. It should be clarified that L¯ is directed from the axis of rotation to the point of application of the force F¯.
The above expression is a vector product. Its resulting vector (M¯) will be perpendicular to the plane formed by L¯ and F¯. To determine the direction of the moment M¯, there are several rules (right hand, gimlet). In order not to memorize them and not get confused in the order of multiplication of the vectors L¯ and F¯ (the direction of M¯ depends on it), you should remember one simple thing: the moment of force will be directed in such a way that if you look from the end of its vector, then the acting forceF¯ will rotate the lever counterclockwise. This direction of the moment is conditionally taken as positive. If the system rotates clockwise, then the resulting moment of forces has a negative value.
Thus, in the considered case with the lever L, the value of M¯ is directed upwards (from the picture to the reader).
In scalar form, the formula for the moment is written as: M=LFsin(180-Φ) or M=LFsin(Φ) (sin(180-Φ)=sin(Φ)). According to the definition of the sine, we can write the equality: M=dF, where d=Lsin(Φ) (see the figure and the corresponding right triangle). The last formula is similar to the one given in the previous paragraph.
The above calculations demonstrate how to work with vector and scalar quantities of moments of forces in order to avoid mistakes.
Physical meaning of M¯
Since the two cases discussed in the previous paragraphs are associated with rotational motion, we can guess what meaning the moment of force has. If the force acting on a material point is a measure of the increase in the speed of the linear displacement of the latter, then the moment of force is a measure of its rotational ability in relation to the system under consideration.
Let's give an illustrative example. Any person opens the door by holding its handle. It can also be done by pushing the door in the area of the handle. Why doesn't anyone open it by pushing in the hinge area? Very simple: the closer the force is applied to the hinges, the more difficult it is to open the door, and vice versa. Conclusion of the previous sentencefollows from the formula for the moment (M=dF), which shows that at M=const, the values d and F are inversely related.

Moment of force is an additive quantity
In all the cases considered above, there was only one acting force. When solving real problems, the situation is much more complicated. Usually systems that rotate or are in equilibrium are subject to several torsional forces, each of which creates its own moment. In this case, the solution of problems is reduced to finding the total moment of forces relative to the axis of rotation.
The total moment is found by the usual sum of the individual moments for each force, however, remember to use the correct sign for each.
Example of problem solving
To consolidate the acquired knowledge, it is proposed to solve the following problem: it is necessary to calculate the total moment of force for the system shown in the figure below.

We see that three forces (F1, F2, F3) act on a lever 7 m long, and they have different points of application relative to the axis of rotation. Since the direction of forces is perpendicular to the lever, there is no need to use a vector expression for the moment of torsion. It is possible to calculate the total moment M using a scalar formula and remembering to set the desired sign. Since the forces F1 and F3 tend to turn the lever counterclockwise, and F2 - clockwise, the moment of rotation for the first will be positive, and for the second - negative. We have: M=F17-F25+F33=140-50+75=165 Nm. That is, the total moment is positive and directed upwards (at the reader).






