Mathematical problems are used in many sciences. These include not only physics, chemistry, engineering and economics, but also medicine, ecology and other disciplines. One of the important concepts that should be mastered in order to find solutions to important dilemmas is the derivative of a function. The physical meaning of it is not at all as difficult to explain as it may seem to the uninitiated in the essence of the issue. It is enough just to find suitable examples of this in real life and ordinary everyday situations. In fact, any motorist copes with a similar task every day when he looks at the speedometer, determining the speed of his car at a particular instant of a fixed time. After all, it is in this parameter that the essence of the physical meaning of the derivative lies.

How to find speed
Determine the speed of a person on the road, knowing the distance traveled and travel time, any fifth grader can easily. To do this, the first of the given values \u200b\u200bis divided by the second. Butnot every young mathematician knows that he is currently finding the ratio of increments of a function and an argument. Indeed, if we imagine the movement in the form of a graph, plotting the path along the y-axis, and the time along the abscissa, it will be exactly like this.
However, the speed of a pedestrian or any other object that we determine on a large section of the path, considering the movement to be uniform, may well change. There are many forms of motion in physics. It can be performed not only with a constant acceleration, but slow down and increase in an arbitrary way. It should be noted that in this case the line describing the movement will no longer be a straight line. Graphically, it can take on the most complex configurations. But for any of the points on the graph, we can always draw a tangent represented by a linear function.
To clarify the parameter of displacement change depending on time, it is necessary to shorten the measured segments. When they become infinitely small, the calculated speed will be instantaneous. This experience helps us to define the derivative. Its physical meaning also follows logically from such reasoning.
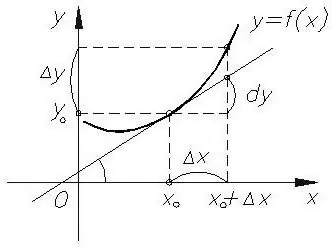
In terms of geometry
It is known that the greater the speed of the body, the steeper the graph of the dependence of displacement on time, and hence the angle of inclination of the tangent to the graph at a certain point. An indicator of such changes can be the tangent of the angle between the x-axis and the tangent line. It just determines the value of the derivative and is calculated by the ratio of lengthsopposite to the adjacent leg in a right triangle formed by a perpendicular dropped from some point to the x-axis.
This is the geometric meaning of the first derivative. The physical one is revealed in the fact that the value of the opposite leg in our case is the distance traveled, and the adjacent one is the time. Their ratio is speed. And again we come to the conclusion that the instantaneous speed, determined when both gaps tend to infinitely small, is the essence of the concept of the derivative, indicating its physical meaning. The second derivative in this example will be the acceleration of the body, which in turn demonstrates the rate of change in speed.

Examples of finding derivatives in physics
The derivative is an indicator of the rate of change of any function, even when we are not talking about movement in the literal sense of the word. To demonstrate this clearly, let's take a few concrete examples. Suppose the current strength, depending on time, changes according to the following law: I=0, 4t2. It is required to find the value of the rate at which this parameter changes at the end of the 8th second of the process. Note that the desired value itself, as can be judged from the equation, is constantly increasing.
To solve it, you need to find the first derivative, the physical meaning of which was considered earlier. Here dI / dt=0.8t. Next, we find it at t \u003d 8, we get that the rate at which the current strength changes is 6.4 A / c. Here it is considered thatcurrent is measured in amperes, and time, respectively, in seconds.
Everything changes
The visible surrounding world, consisting of matter, is constantly undergoing changes, being in motion of various processes occurring in it. A variety of parameters can be used to describe them. If they are united by dependence, then they are mathematically written as a function that clearly shows their changes. And where there is movement (in whatever form it is expressed), there is also a derivative, the physical meaning of which we are considering at the moment.

On this occasion, the following example. Suppose the body temperature changes according to the law T=0, 2 t 2. You should find the rate of its heating at the end of the 10th second. The problem is solved in a manner similar to that described in the previous case. That is, we find the derivative and substitute the value for t \u003d 10 into it, we get T \u003d 0, 4 t \u003d 4. This means that the final answer is 4 degrees per second, that is, the heating process and the temperature change, measured in degrees, occurs precisely with at such a speed.
Solving practical problems
Of course, in real life everything is much more complicated than in theoretical problems. In practice, the value of quantities is usually determined during the experiment. In this case, instruments are used that give readings during measurements with a certain error. Therefore, in calculations, one has to deal with approximate values of the parameters and resort to rounding inconvenient numbers,as well as other simplifications. Having taken this into account, we will again proceed to problems on the physical meaning of the derivative, given that they are only a kind of mathematical model of the most complex processes occurring in nature.
Volcano Eruption
Let's imagine that a volcano erupts. How dangerous can he be? To answer this question, many factors need to be considered. We will try to accommodate one of them.

From the mouth of the "fiery monster" stones are thrown vertically upwards, having an initial speed of 120 m/s from the moment they exit. It is necessary to calculate what they can reach the maximum height.
To find the desired value, we will compose an equation for the dependence of the height H, measured in meters, on other values. These include initial speed and time. The acceleration value is considered known and approximately equal to 10 m/s2.

Partial derivative
Now let's consider the physical meaning of the derivative of a function from a slightly different angle, because the equation itself can contain not one, but several variables. For example, in the previous problem, the dependence of the height of the rise of stones ejected from the vent of a volcano was determined not only by the change in time characteristics, but also by the value of the initial velocity. The latter was considered a constant, fixed value. But in other tasks with completely different conditions, everything could be different. If the quantities on which the complexfunction, several, calculations are made according to the formulas below.
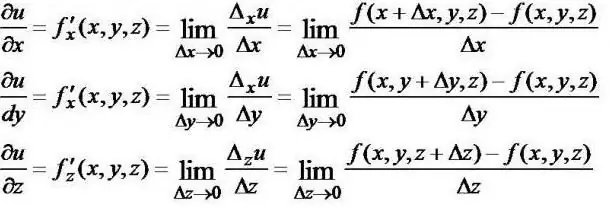
The physical meaning of the frequent derivative should be determined as in the usual case. This is the rate at which the function changes at some particular point as the parameter of the variable increases. It is calculated in such a way that all other components are taken as constants, only one is considered as a variable. Then everything happens according to the usual rules.
Indispensable adviser on many issues
Understanding the physical meaning of the derivative, it is not difficult to give examples of solving intricate and complex problems, in which the answer can be found with such knowledge. If we have a function that describes the fuel consumption depending on the speed of the car, we can calculate at what parameters of the latter the gasoline consumption will be the least.
In medicine, you can predict how the human body will react to a medicine prescribed by a doctor. Taking the drug affects a variety of physiological parameters. These include changes in blood pressure, heart rate, body temperature, and more. All of them depend on the dose of the drug taken. These calculations help to predict the course of treatment, both in favorable manifestations and in undesirable accidents that can fatally affect changes in the patient's body.

Undoubtedly, it is important to understand the physical meaning of the derivative in technicalissues, in particular in electrical engineering, electronics, design and construction.
Braking distance
Let's consider the next problem. Moving at a constant speed, the car, approaching the bridge, had to slow down 10 seconds before the entrance, as the driver noticed a road sign prohibiting movement at a speed of more than 36 km/h. Did the driver violate the rules if the braking distance can be described by the formula S=26t - t2?
Calculating the first derivative, we find the formula for the speed, we get v=28 - 2t. Next, substitute the value t=10 into the specified expression.
Since this value was expressed in seconds, the speed is 8 m/s, which means 28.8 km/h. This makes it possible to understand that the driver started to slow down in time and did not violate the traffic rules, and hence the limit indicated on the speed sign.
This proves the importance of the physical meaning of the derivative. An example of solving this problem demonstrates the breadth of the use of this concept in various spheres of life. Including in everyday situations.

Derivative in economics
Until the 19th century, economists mostly operated on averages, whether it was labor productivity or the price of output. But from some point on, limiting values became more necessary for making effective forecasts in this area. These include marginal utility, income or cost. Understanding this gave impetus to the creation of a completely new tool in economic research,which has existed and developed for more than a hundred years.
To make such calculations, where such concepts as minimum and maximum predominate, it is simply necessary to understand the geometric and physical meaning of the derivative. Among the creators of the theoretical basis of these disciplines, one can name such prominent English and Austrian economists as W. S. Jevons, K. Menger and others. Of course, limit values in economic calculations are not always convenient to use. And, for example, quarterly reports do not necessarily fit into the existing scheme, but still, the application of such a theory in many cases is useful and effective.






