People are accustomed to taking the obvious for granted. Because of this, they often get into trouble, misjudging the situation, trusting their intuition and not taking the time to critically reflect on their choice and its consequences.
What is the Monty Hall Paradox? This is a clear illustration of the inability of a person to weigh his chances of success in the face of choosing a favorable outcome in the presence of more than one unfavorable one.
Formulation of the Monty Hall Paradox
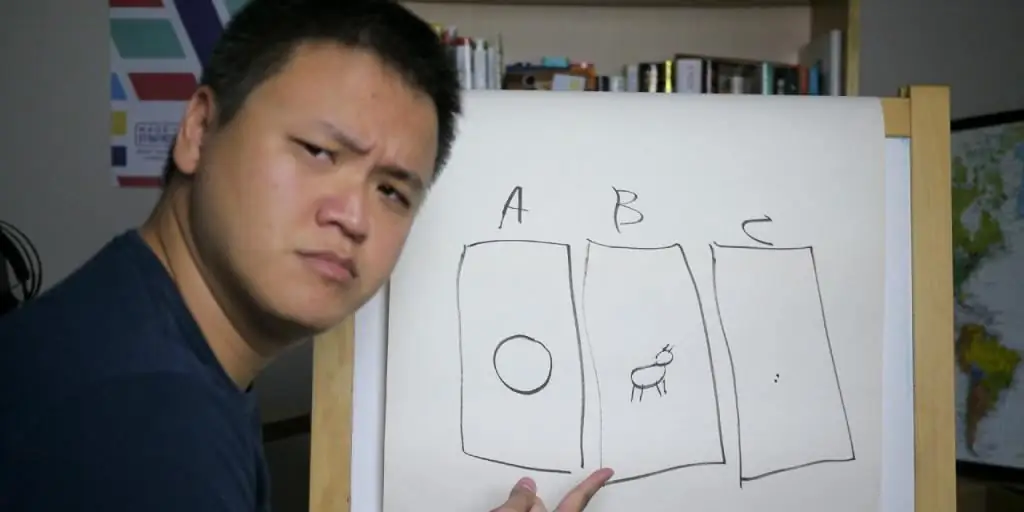
So, what kind of animal is this? What, exactly, are we talking about? The most famous example of the Monty Hall paradox is the television show popular in America in the middle of the last century called Let's Make a Bet! By the way, it was thanks to the presenter of this quiz that the Monty Hall paradox later got its name.

The game consisted of the following: the participant was shown three doors that looked exactly the same. However, behind one of them, an expensive new car was waiting for the player, but behind the other two, a goat languished impatiently. As is usually the case in the case of TV quizzes, what was behind the door chosen by the contestant became hiswinning.
What is the trick?

But not everything is so simple. After the choice was made, the host, knowing where the main prize was hidden, opened one of the remaining two doors (of course, the one behind which the artiodactyl lurked), and then asked the player if he wanted to change his mind.
Monty Hall's paradox, formulated by scientists in 1990, is that, contrary to the intuition that there is no difference in making a leading decision based on a question, one must agree to change one's choice. If you want to get a great car, of course.
How does it work?
There are several reasons why people will not want to give up their choice. Intuition and simple (but incorrect) logic say that nothing depends on this decision. Moreover, not everyone wants to follow the lead of another - this is real manipulation, isn't it? No not like this. But if everything were immediately intuitively clear, then they would not even call it a paradox. There is nothing strange about having doubts. When this puzzle was first published in one of the major journals, thousands of readers, including recognized mathematicians, sent letters to the editor claiming that the answer printed in the issue was not true. If the existence of the theory of probability was not news to a person who got on the show, then perhaps he would be able to solve this problem. And thereby increase the chancesto win. In fact, the explanation of the Monty Hall paradox comes down to simple mathematics.
Explanation one, more complicated
The probability that the prize is behind the door that was originally chosen is one in three. The chance of finding it behind one of the two remaining is two out of three. Logical, right? Now, after one of these doors is open, and a goat is found behind it, only one option remains in the second set (the one that corresponds to 2/3 chance of success). The value of this option remains the same, and it is equal to two out of three. Thus, it becomes obvious that by changing his decision, the player will double the probability of winning.
Explanation number two, simpler
After such an interpretation of the decision, many still insist that there is no point in this choice, because there are only two options and one of them is definitely winning, and the other definitely leads to defeat.
But the theory of probability has its own view on this problem. And this becomes even clearer if we imagine that initially there were not three doors, but, say, a hundred. In this case, the chance of guessing where the prize is from the first time is only one in ninety-nine. Now the contestant makes his choice, and Monty eliminates ninety-eight goat doors, leaving only two, one of which the player has chosen. Thus, the option chosen initially keeps the odds of winning equal to 1/100, while the second option offered is 99/100. The choice should be obvious.
Are there rebuttals?
The answer is simple: no. No oneThere is no well-founded refutation of the Monty Hall paradox. All "revelations" that can be found on the Web come down to a misunderstanding of the principles of mathematics and logic.
For anyone who is familiar with mathematical principles, the non-randomness of probabilities is absolutely obvious. Only those who do not understand how logic works can disagree with them. If all of the above still sounds unconvincing - the rationale for the paradox was tested and confirmed on the famous MythBusters program, and who else to believe if not them?

The ability to see clearly
Okay, let's all sound convincing. But this is only a theory, is it possible to somehow look at the work of this principle in action, and not just in words? First, no one canceled living people. Find a partner who will take on the role of leader and help you play the above algorithm in reality. For convenience, you can take boxes, boxes, or even draw on paper. After repeating the process several dozen times, compare the number of wins in the case of changing the original choice with how many wins brought stubbornness, and everything will become clear. And you can do even easier and use the Internet. There are many simulators of the Monty Hall paradox on the Web, in which you can check everything yourself and without unnecessary props.
What is the use of this knowledge?
It might seem like just another brain-teasing puzzle, and it's just for entertainment purposes. However, its practical applicationMonty Hall's paradox is found primarily in gambling and various sweepstakes. Those who have extensive experience are well aware of the common strategies for increasing the chances of finding a value bet (from the English word value, which literally means "value" - such a prediction that will come true with a higher probability than bookmakers estimated). And one such strategy directly engages Monty Hall's paradox.
Example of working with a totalizator

A sports example will differ little from the classic one. Let's say there are three teams from the first division. In the next three days, each of these teams must play one decisive match. The one that scores more points at the end of the match than the other two will remain in the first division, while the rest will be forced to leave it. The bookmaker's offer is simple: you need to bet on the preservation of the positions of one of these football clubs, while the odds of bets are equal.
For convenience, conditions are accepted under which the rivals of the clubs participating in the selection are approximately equal in strength. Thus, it will not be possible to unequivocally determine the favorite before the start of the games.
Here you need to remember the story about the goats and the car. Each team has a chance to stay in its place in one case out of three. Any of them is chosen, a bet is placed on it. Let it be "B altika". According to the results of the first day, one of the clubs is losing, and two have yet to play. This is the same "B altika" and, say, "Shinnik".
The majority will retain their original bet - B altika will remain in the first division. But it should be remembered that her chances remained the same, but the chances of “Shinnik” have doubled. Therefore, it is logical to make another bet, a larger one, on the victory of “Shinnik”.
The next day comes, and the match with B altika is a draw. “Shinnik” plays next, and his game ends with a 3-0 victory. It turns out that he will remain in the first division. Therefore, although the first bet on B altika is lost, this loss is covered by the profit on the new bet on Shinnik.
It can be assumed, and most will do so, that the victory of “Shinnik” is just an accident. In fact, taking probability for chance is the biggest mistake for a person participating in sports sweepstakes. After all, a professional will always say that any probability is expressed primarily in clear mathematical patterns. If you know the basics of this approach and all the nuances associated with it, then the risks of losing money will be minimized.
Useful in predicting economic processes
So, in sports betting, the Monty Hall paradox is simply necessary to know. But the scope of its application is not limited to one sweepstakes. Probability theory is always closely related to statistics, which is why understanding the principles of paradox is no less important in politics and economics.
In the face of economic uncertainty that analysts often deal with, one should remember the following stemming fromproblem solving conclusion: it is not necessary to know exactly the only correct solution. The chances of a successful forecast always increase if you know what exactly will not happen. Actually, this is the most useful conclusion from the Monty Hall paradox.
When the world is on the verge of economic shocks, politicians always try to guess the right course of action in order to minimize the consequences of the crisis. Returning to the previous examples, in the field of economics, the task can be described as follows: there are three doors in front of the leaders of the countries. One leads to hyperinflation, the second to deflation, and the third to the coveted moderate growth of the economy. But how do you find the right answer?
Politicians claim that one way or another they will lead to more jobs and growth of the economy. But leading economists, experienced people, including even Nobel Prize winners, clearly demonstrate to them that one of these options will definitely not lead to the desired result. Will politicians change their choice after this? It is highly unlikely, since in this respect they are not much different from the same participants in the TV show. Therefore, the probability of error will only increase with the increase in the number of advisers.
Does this exhaust information on the topic?
In fact, so far only the "classic" version of the paradox has been considered here, that is, the situation in which the presenter knows exactly which door the prize is behind and opens only the door with the goat. But there are other mechanisms of behavior of the leader, depending on which the principle of operation of the algorithm and the result of its execution will bebe different.
The influence of the leader's behavior on the paradox

So what can the host do to change the course of events? Let's allow different options.
The so-called "Devil Monty" is a situation in which the host will always offer the player to change his choice, provided that he was initially correct. In this case, changing the decision will always lead to defeat.
On the contrary, "Angelic Monty" is a similar principle of behavior, but in the event that the player's choice was initially incorrect. It is logical that in such a situation, changing the decision will lead to victory.
If the host opens the doors at random, having no idea what is hidden behind each of them, then the chances of winning will always be equal to fifty percent. In this case, a car may also be behind the open leading door.
The host can 100% open the door with a goat if the player has chosen a car, and with a 50% chance if the player has chosen a goat. With this algorithm of actions, if the player changes the choice, he will always win in one case out of two.
When the game is repeated over and over again, and the probability that a certain door will be the winner is always arbitrary (as well as which door the host opens, while he knows where the car is hiding, and he always opens the door with a goat and offers to change the choice) - the chance to win will always be equal to one out of three. This is called the Nash equilibrium.
As well as in the same case, but on the condition that the presenter is not obliged to openone of the doors at all - the probability of winning will still be 1/3.
While the classical scheme is fairly easy to test, experiments with other possible leader behavior algorithms are much more difficult to perform in practice. But with due meticulousness of the experimenter, this is also possible.
And yet, what's the point of all this?

Understanding the mechanisms of action of any logical paradoxes is very useful for a person, his brain and understanding how the world can actually work, how much its structure can differ from the usual idea of an individual about it.
The more a person knows about how things around him work in everyday life and what he is not used to thinking about at all, the better his consciousness works, and the more effective he can be in his actions and aspirations.






