Bertrand's paradox is a problem in the classical interpretation of probability theory. Joseph introduced it in his work Calcul des probabilités (1889) as an example that probabilities cannot be well defined if a mechanism or method produces a random variable.
Problem Statement
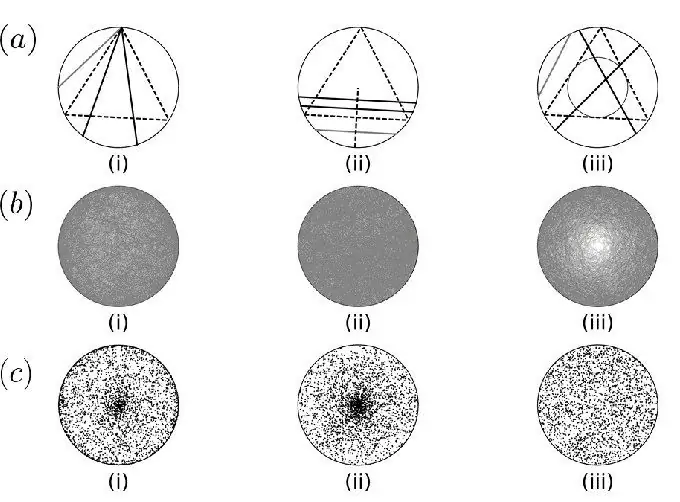
Bertrand's paradox is as follows.
First, consider an equilateral triangle inscribed in a circle. In this case, the diameter is chosen randomly. What is the probability that it is longer than the side of the triangle?
Bertrand made three arguments, all of which appear to be correct, but give different results.
Random Endpoint Method

You need to select two places on the circle and draw an arc connecting them. For the calculation, Bertrand's probability paradox is considered. It is necessary to imagine that the triangle is rotated so that its vertex coincides with one of the endpoints of the chord. Worth payingnote that if the other part is on an arc between two places, the circle is longer than the side of the triangle. The length of the arc is one third of the circle, so the probability that a random chord is longer is 1/3.
Selection method
It is necessary to select the radius of the circle and a point on it. After that, you need to build a chord through this place, perpendicular to the diameter. To calculate the considered paradox of Bertrand of probability theory, one must imagine that the triangle is rotated so that the side is perpendicular to the radius. The chord is longer than the leg if the selected point is closer to the center of the circle. And in this case, the side of the triangle bisects the radius. Therefore, the probability that the chord is longer than the side of the inscribed figure is 1/2.
Random chords
Midpoint method. It is necessary to choose a place on the circle and create a chord with a given middle. The axis is longer than the edge of the inscribed triangle, if the selected location is within a concentric circle of radius 1/2. The area of the smaller circle is one fourth of the larger figure. Therefore, the probability of a random chord is longer than the side of the inscribed triangle and equals 1/4.
As presented above, selection methods differ in the weight they give to certain chords, which are diameters. In method 1, each chord can be selected in exactly one way, regardless of whether it is a diameter.
In method 2, each straight line can be selected in two ways. Whereas any other chord will be chosenonly one of the possibilities.
In method 3, each midpoint selection has a single parameter. Except for the center of the circle, which is the midpoint of all diameters. These problems can be avoided by "ordering" all questions to exclude parameters without affecting the resulting probabilities.
Select methods can also be visualized as follows. A chord that is not a diameter is uniquely identified by its midpoint. Each of the three selection methods presented above produces a different distribution of the middle. And options 1 and 2 provide two different non-uniform partitions, while method 3 gives a uniform distribution.
The classic paradox of solving Bertrand's problem depends on the method by which the chord is chosen "at random". It turns out that if a method of random selection is specified in advance, the problem has a well-defined solution. This is because each individual method has its own distribution of chords. The three rulings shown by Bertrand correspond to different modes of selection and, in the absence of further information, there is no reason to favor one over the other. Accordingly, the stated problem does not have a single solution.
An example of how to make a general answer unique is to specify that the endpoints of the chord are evenly spaced between 0 and c, where c is the circumference of the circle. This distribution is the same as in Bertrand's first argument and the resulting unique probability will be 1/3.
This Bertrand Russell paradox and other uniquenesses of classicalinterpretations of possibility justify more rigorous formulations. Including probability frequency and subjectivist Bayesian theory.
What underlies Bertrand's Paradox

In his 1973 article "The Well-Pposed Problem," Edwin Jaynes offered his unique solution. He noted that Bertrand's paradox is based on a premise based on the principle of "maximum ignorance". This means that you should not use any information that is not provided in the problem statement. Jaynes pointed out that Bertrand's problem does not determine the position or size of the circle. And argued that therefore any definite and objective decision must be "indifferent" to size and position.
For illustration purposes
Assuming that all the chords are placed randomly on a 2 cm circle, now you need to throw straws at it from afar.
Then you need to take another circle with a smaller diameter (for example, 1 centimeter), which fits into a larger figure. Then the distribution of chords on this smaller circle should be the same as on the maximum one. If the second figure also moves inside the first, the probability, in principle, should not change. It is very easy to see that for method 3 the following change will occur: the distribution of chords on the small red circle will be qualitatively different from the distribution on the large circle.
The same happens for method 1. Although it's harder to see in the graphical view.
Method 2 is the only onewhich turns out to be both a scale and a translation invariant.
Method number 3 seems to be simply extensible.
Method 1 is neither.
However, Janes did not use invariants easily to accept or reject these methods. This would leave the possibility that there is another undescribed method that would fit its aspects of reasonable meaning. Jaynes applied integral equations describing invariances. To directly determine the probability distribution. In his problem, the integral equations do indeed have a unique solution, and this is exactly what was called the second random radius method above.
In a 2015 paper, Alon Drory argues that Jaynes' principle can also yield two other Bertrand solutions. The author assures that the mathematical implementation of the above properties of invariance is not unique, but depends on the basic random selection procedure that a person decides to use. He shows that each of the three Bertrand solutions can be obtained using rotational, scaling, and translational invariance. At the same time, concluding that the Jaynes principle is just as subject to interpretation as the mode of indifference itself.
Physical experiments

Method 2 is the only solution that satisfies the transformation invariants that are present in specific physiological concepts such as statistical mechanics and gas structure. Also in the proposedJanes' experiment of throwing straws from a small circle.
However, other practical experiments can be designed that provide answers according to other methods. For example, to arrive at a solution to the first random endpoint method, you can attach a counter to the center of the area. And let the results of two independent rotations highlight the final places of the chord. To arrive at a solution to the third method, one can cover the circle with molasses, for example, and mark the first point on which the fly lands as the middle chord. Several contemplators have created studies to draw different conclusions and have confirmed the results empirically.
Latest events
In his 2007 article "The Bertrand Paradox and the Indifference Principle," Nicholas Shackel argues that more than a century later, the problem still remains unresolved. She goes on to refute the principle of indifference. Furthermore, in his 2013 paper, "The Bertrand Russell Paradox Revisited: Why All Solutions Are Not Practical," Darrell R. Robottom shows that all of the proposed rulings have nothing to do with his own question. So it turned out that the paradox would be much more difficult to solve than previously thought.
Shackel emphasizes that so far many scientists and people far from science have tried to resolve Bertrand's paradox. It is still overcome with the help of two different approaches.
Those in which the difference between non-equivalent problems was considered, and those in which the problem was always considered correct. Shackel quotes Louis in his booksMarinoff (as a typical exponent of the strategy of differentiation) and Edwin Jaynes (as the author of a well-thought-out theory).
However, in their recent work Solving a Complex Problem, Diederik Aerts and Massimiliano Sassoli de Bianchi believe that in order to solve the Bertrand paradox, the premises must be sought in a mixed strategy. According to these authors, the first step is to fix the problem by clearly stating the nature of the entity being randomized. And only after this is done, any problem can be considered correct. That's what Janes thinks.
So the principle of maximum ignorance can be used to solve it. To this end, and since the problem does not specify how a chord should be chosen, the principle is applied not at the level of the various possibilities, but at a much deeper one.
Selection of parts

This part of the problem requires the calculation of a meta-average over all possible ways, which the authors call the universal mean. To deal with this, they use the discretization method. Inspired by what is being done in defining the law of probability in Wiener processes. Their result is consistent with the numerical corollary of Jaynes, although their well-posed problem differs from the original author's one.
In economics and commerce, the Bertrand paradox, named after its creator Joseph Bertrand, describes a situation in which two players (firms) reach a Nash equilibrium. When both firms set a price equal to marginal cost(MS).
Bertrand's paradox is based on a premise. It lies in the fact that in models such as Cournot competition, an increase in the number of firms is associated with the convergence of prices with marginal costs. In these alternative models, Bertrand's paradox is in an oligopoly of a small number of firms that earn positive profits by charging prices above cost.
To begin with, it is worth assuming that two firms A and B sell a homogeneous product, each of which has the same cost of production and distribution. It follows that buyers choose a product solely on the basis of price. This means that demand is infinitely price elastic. Neither A nor B will set a higher price than the others, because that will cause the whole Bertrand paradox to collapse. One of the market participants will yield to its competitor. If they set the same price, the companies will share the profits.
On the other hand, if any firm lowers its price even slightly, it will get the whole market and a significantly higher return. Since A and B know this, they will each try to undercut the competitor until the product sells for zero economic profit.
Recent work has shown that there may be an additional equilibrium in Bertrand's mixed strategy paradox, with positive economic profits, provided that the monopoly sum is infinite. For the case of final profit, it was shown that a positive increase under price competition is impossible in mixed equilibria and even in the more general casecorrelated systems.
In fact, Bertrand's paradox in economics is rarely seen in practice, because real products are almost always differentiated in some way other than price (for example, overpaying for a label). Firms have limits on their ability to produce and distribute. This is why two businesses rarely have the same costs.
Bertrand's result is paradoxical because if the number of firms increases from one to two, the price drops from monopoly to competitive and remains at the same level as the number of firms that increase thereafter. This is not very realistic, because in reality, markets with few firms with market power tend to charge prices above marginal cost. Empirical analysis shows that most industries with two competitors generate positive profits.
In the modern world, scientists are trying to find solutions to the paradox that are more consistent with the Cournot model of competition. Where two firms in a market are making positive profits that are somewhere between perfectly competitive and monopoly levels.
Some reasons why Bertrand's paradox is not directly related to economics:
- Capacity limits. Sometimes firms do not have sufficient capacity to meet all demand. This point was first raised by Francis Edgeworth and gave rise to the Bertrand-Edgeworth model.
- Integer prices. Prices above the MC are excluded because one firm can undercut another at random.a small amount. If prices are discrete (for example, they must take integer values), then one firm must undercut the other by at least one ruble. This implies that the value of the petty currency is above the MC. If another firm sets the price for it higher, another firm can lower it and capture the entire market, Bertrand's paradox consists precisely in this. It won't bring her any profit. This business will prefer to share sales 50/50 with another firm and receive a purely positive revenue.
- Product differentiation. If the products of different firms differ from each other, then consumers may not fully switch to products with a lower price.
- Dynamic competition. Repeated interaction or repeated price competition can lead to an equilibrium of value.
- More items for a higher amount. This follows from repeated interaction. If one company sets its price a little higher, it will still get roughly the same number of purchases, but more profit per item. Therefore, the other company will increase its markup, etc. (Only in replays, otherwise the dynamics goes in the other direction).
Oligopoly

If two companies can agree on a price, it is in their long-term interests to keep the agreement: value reduction revenue is less than twice the revenue from compliance with the agreement and lasts only until the other firm cuts its own prices.
Theoryprobabilities (like the rest of mathematics) is actually a recent invention. And development has not been smooth. The first attempts to formalize the calculus of probability were made by the Marquis de Laplace, who proposed to define the concept as the ratio of the number of events leading to an outcome.
This, of course, only makes sense if the number of all possible events is finite. And besides, all events are equally likely.
Thus, at the time, these concepts seemed to have no solid foundation. Attempts to extend the definition to the case of an infinite number of events have led to even greater difficulties. Bertrand's paradox is one such discovery that has made mathematicians wary of the whole concept of probability.






