The phenomenon of wave diffraction is one of the effects that reflects the wave nature of light. It was for light waves that it was discovered at the beginning of the 19th century. In this article, we will look at what this phenomenon is, how it is described mathematically, and where it finds application.
Wave diffraction phenomenon
As you know, any wave, be it light, sound or disturbances on the surface of water, in a homogeneous medium propagates along a straight path.
Let's imagine a wave front that has a flat surface and moves in a certain direction. What will happen if there is an obstacle in the way of this front? Anything can serve as an obstacle (a stone, a building, a narrow gap, and so on). It turns out that after passing through the obstacle, the wave front will no longer be flat, but will take on a more complex shape. So, in the case of a small round hole, the wave front, passing through it, becomes spherical.
The phenomenon of changing the direction of wave propagation when it encounters an obstacle in its path is called diffraction (diffractus from Latin means"broken").
The result of this phenomenon is that the wave penetrates into the space behind the obstacle, where it would never hit in its rectilinear motion.
An example of wave diffraction on a seashore is shown in the figure below.

Diffraction observation conditions
The above-described effect of wave breaking when passing an obstacle depends on two factors:
- wavelength;
- geometric parameters of the obstacle.
Under what condition is wave diffraction observed? For a better understanding of the answer to this question, it should be noted that the phenomenon under consideration always occurs when a wave encounters an obstacle, but it becomes noticeable only when the wavelength is of the order of the geometric parameters of the obstacle. Since the wavelengths of light and sound are small compared to the size of the objects around us, the diffraction itself appears only in some special cases.
Why does wave diffraction occur? This can be understood if we consider the Huygens-Fresnel principle.
Huygens principle
In the middle of the 17th century, the Dutch physicist Christian Huygens put forward a new theory of the propagation of light waves. He believed that, like sound, light moves in a special medium - ether. A light wave is a vibration of ether particles.
Considering a wave spherical front created by a point light source, Huygens came to the following conclusion: in the process of motion, the front passes through a series of spatial points inbroadcast. As soon as he reaches them, he makes him hesitate. The oscillating points, in turn, generate a new generation of waves, which Huygens called secondary. From each point the secondary wave is spherical, but it alone does not define the surface of the new front. The latter is the result of superposition of all spherical secondary waves.
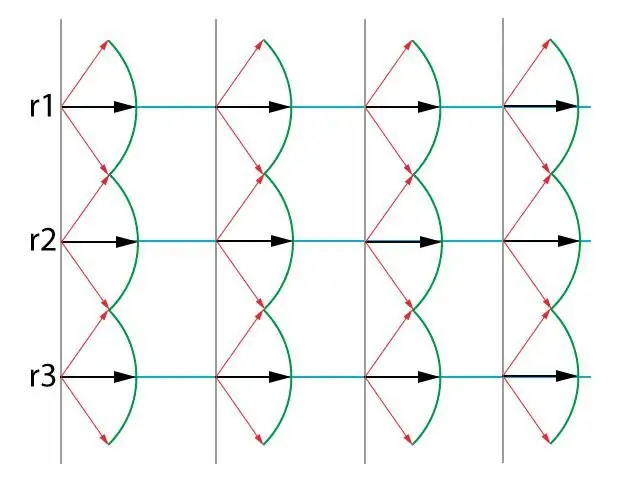
The effect described above is called the Huygens principle. He does not explain the diffraction of waves (when the scientist formulated it, they did not yet know about the diffraction of light), but he successfully describes such effects as the reflection and refraction of light.
As Newton's corpuscular theory of light triumphed in the 17th century, Huygens' work was forgotten for 150 years.
Thomas Jung, Augustin Fresnel and the revival of the Huygens principle
The phenomenon of diffraction and interference of light was discovered in 1801 by Thomas Young. Carrying out experiments with two slits through which a monochromatic light front passed, the scientist received on the screen a picture of alternating dark and light stripes. Jung fully explained the results of his experiments, referring to the wave nature of light, and thus confirming Maxwell's theoretical calculations.
As soon as Newton's corpuscular theory of light was refuted by Young's experiments, the French scientist Augustin Fresnel remembered Huygens' work and used his principle to explain the phenomenon of diffraction.
Fresnel believed that if an electromagnetic wave, propagating in a straight line, meets an obstacle, then part of its energy is lost. The rest is spent on the formation of secondary waves. The latter lead to the emergence of a new wave front, the direction of propagation of which differs from the original one.
The described effect, which does not take into account the ether when generating secondary waves, is called the Huygens-Fresnel principle. He successfully describes the diffraction of waves. Moreover, this principle is currently used to determine the energy losses during the propagation of electromagnetic waves in the path of which an obstacle is encountered.

Narrow slit diffraction
The theory of constructing diffraction patterns is quite complex from a mathematical point of view, since it involves the solution of Maxwell's equations for electromagnetic waves. Nevertheless, the Huygens-Fresnel principle, as well as a number of other approximations, make it possible to obtain mathematical formulas suitable for their practical application.
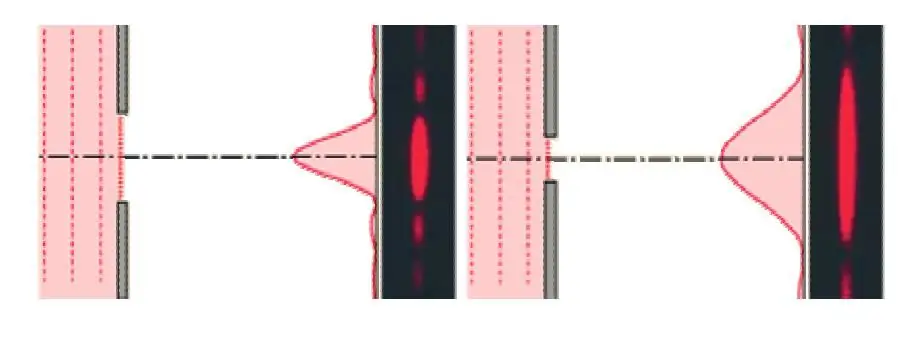
If we consider diffraction on a thin slit, on which a plane wave front falls parallel, then bright and dark stripes will appear on a screen located far from the slit. The minima of the diffraction pattern in this case are described by the following formula:
ym=mλL/a, where m=±1, 2, 3, …
Here ym is the distance from the slit projection onto the screen to the minimum of order m, λ is the light wavelength, L is the distance to the screen, a is the slit width.
It follows from the expression that the central maximum will be more blurry if the slit width is decreased andincrease the wavelength of light. The figure below shows what the corresponding diffraction pattern would look like.
Diffraction grating
If a combination of slots from the example above is applied to one plate, then the so-called diffraction grating will be obtained. Using the Huygens-Fresnel principle, one can obtain a formula for the maxima (bright bands) that are obtained when light passes through the grating. The formula looks like this:
sin(θ)=mλ/d, where m=0, ±1, 2, 3, …
Here, the parameter d is the distance between the nearest slots on the grating. The smaller this distance, the greater the distance between the bright bands in the diffraction pattern.
Since the angle θ for the m-th order maxima depends on the wavelength λ, when white light passes through a diffraction grating, multi-colored stripes appear on the screen. This effect is used in the manufacture of spectroscopes capable of analyzing the characteristics of the emission or absorption of light by a particular source, such as stars and galaxies.

The Importance of Diffraction in Optical Instruments
One of the main characteristics of instruments such as a telescope or a microscope is their resolution. It is understood as the minimum angle, when observed under which individual objects are still distinguishable. This angle is determined from the wave diffraction analysis according to the Rayleigh criterion using the following formula:
sin(θc)=1, 22λ/D.
Where D is the diameter of the lens of the device.

If we apply this criterion to the Hubble telescope, we get that the device at a distance of 1000 light years is able to distinguish between two objects, the distance between which is similar to that between the Sun and Uranus.






