When studying absolutely any spatial figure, it is important to know how to calculate its volume. This article provides a formula for the volume of a regular quadrangular pyramid, and also shows how this formula should be used using an example of solving problems.
Which pyramid are we talking about?
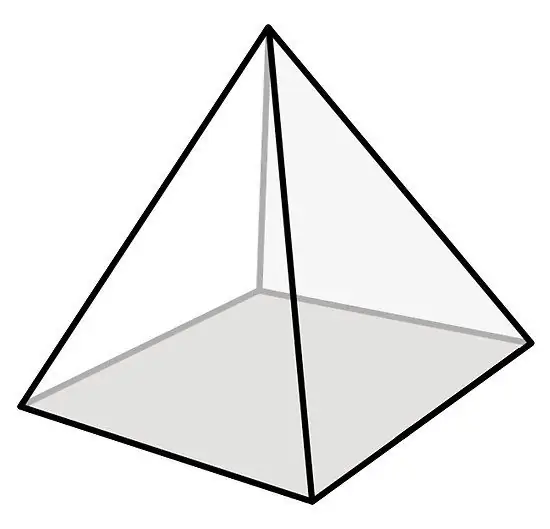
Every high school student knows that a pyramid is a polyhedron consisting of triangles and a polygon. The latter is the base of the figure. Triangles have one common side with the base and intersect at a single point, which is the top of the pyramid.
Each pyramid is characterized by the length of the sides of the base, the length of the side edges and the height. The latter is a perpendicular segment, lowered to the base from the top of the figure.
A regular quadrangular pyramid is a figure with a square base, the height of which intersects this square in its center. Perhaps the most famous example of this type of pyramids are the ancient Egyptian stone structures. Below is a photopyramids of Cheops.

The figure under study has five faces, four of which are identical isosceles triangles. It is also characterized by five vertices, four of which belong to the base, and eight edges (4 edges of the base and 4 edges of the side faces).
The formula for the volume of a quadrangular pyramid is correct

The volume of the figure in question is a part of the space that is limited by five sides. To calculate this volume, we use the following dependence of the area of the slice Sz parallel to the base of the pyramid on the vertical coordinate z:
Sz=So (h - z/h)2
Here So is the area of the square base. If we substitute z=h into the written expression, then we will get a zero value for Sz. This value of z corresponds to a slice that will contain only the top of the pyramid. If z=0, then we get the value of the base area So.

The volume of a pyramid is easy to find, knowing the function Sz(z), for this it is enough to cut the figure into an infinite number of layers parallel to the base, and then carry out the integration operation. I follow this technique, we get:
V=∫0h(Sz)dz=-S 0(h-z)3 / (3h2)|0 h=1/3S0h.
Because S0 isthe area of the square base, then, denoting the side of the square with the letter a, we obtain the formula for the volume of a regular quadrangular pyramid:
V=1/3a2h.
Now let's use examples of problem solving to show how this expression should be applied.
The problem of determining the volume of a pyramid through its apothem and side edge
The apothem of a pyramid is the height of its lateral triangle, which is lowered to the side of the base. Since all triangles are equal in a regular pyramid, their apothems will also be the same. Let's denote its length by the symbol hb. Denote the side edge as b.
Knowing that the apothem of the pyramid is 12 cm, and its lateral edge is 15 cm, find the volume of a regular quadrangular pyramid.
The formula for the figure's volume written in the previous paragraph contains two parameters: side length a and height h. At the moment, we do not know any of them, so let's take a look at their calculations.
The length of the side of a square a is easy to calculate if you use the Pythagorean theorem for a right triangle, in which the hypotenuse is the edge b, and the legs are the apothem hb and half of the side of the base a/2. We get:
b2=hb2+ a2 /4=>
a=2√(b2- hb2).
Substituting the known values from the condition, we get the value a=18 cm.
To calculate the height h of the pyramid, you can do two things: consider a rectangulara triangle with a hypotenuse-lateral edge or with a hypotenuse-apothem. Both methods are equal and involve the performance of the same number of mathematical operations. Let us dwell on the consideration of a triangle, where the hypotenuse is the apothem hb. The legs in it will be h and a / 2. Then we get:
h=√(hb2-a2/4)=√(12 2- 182/4)=7, 937 cm.
Now you can use the formula for volume V:
V=1/3a2h=1/31827, 937=857, 196 cm 3.
Thus, the volume of a regular quadrangular pyramid is approximately 0.86 liters.
The volume of the pyramid of Cheops
Now let's solve an interesting and practically important problem: find the volume of the largest pyramid in Giza. It is known from the literature that the original height of the building was 146.5 meters, and the length of its base is 230.363 meters. These numbers allow us to apply the formula to calculate V. We get:
V=1/3a2h=1/3230, 3632146, 5 ≈ 2591444 m 3.
The resulting value is almost 2.6 million m3. This volume corresponds to the volume of a cube whose side is 137.4 meters.






