Stereometry, as a branch of geometry in space, studies the properties of prisms, cylinders, cones, balls, pyramids and other three-dimensional figures. This article is devoted to a detailed review of the characteristics and properties of a hexagonal regular pyramid.
Which pyramid will be studied
A regular hexagonal pyramid is a figure in space, which is limited by one equilateral and equiangular hexagon, and six identical isosceles triangles. These triangles can also be equilateral under certain conditions. This pyramid is shown below.
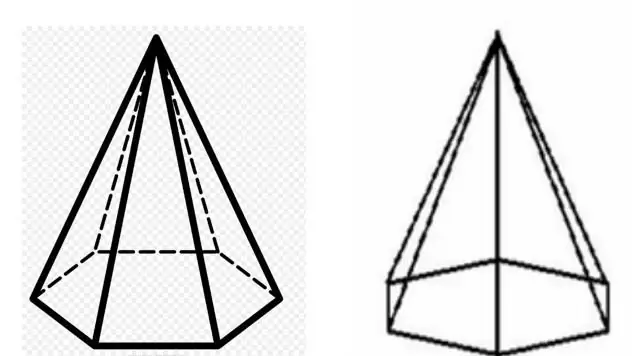
The same figure is shown here, only in one case it is turned with its side face towards the reader, and in the other case it is turned with its side edge.
A regular hexagonal pyramid has 7 faces, which were mentioned above. It also has 7 vertices and 12 edges. Unlike prisms, all pyramids have one special vertex, which is formed by the intersection of the later altriangles. For a regular pyramid, it plays an important role, since the perpendicular lowered from it to the base of the figure is the height. Further, the height will be denoted by the letter h.
The shown pyramid is called correct for two reasons:
- at its base is a hexagon with equal side lengths a and equal angles of 120o;
- The height of the pyramid h intersects the hexagon exactly at its center (the point of intersection lies at the same distance from all sides and from all vertices of the hexagon).
Surface area
Properties of a regular hexagonal pyramid will be considered from the definition of its area. To do this, it is first useful to unfold the figure on a plane. A schematic representation of it is shown below.
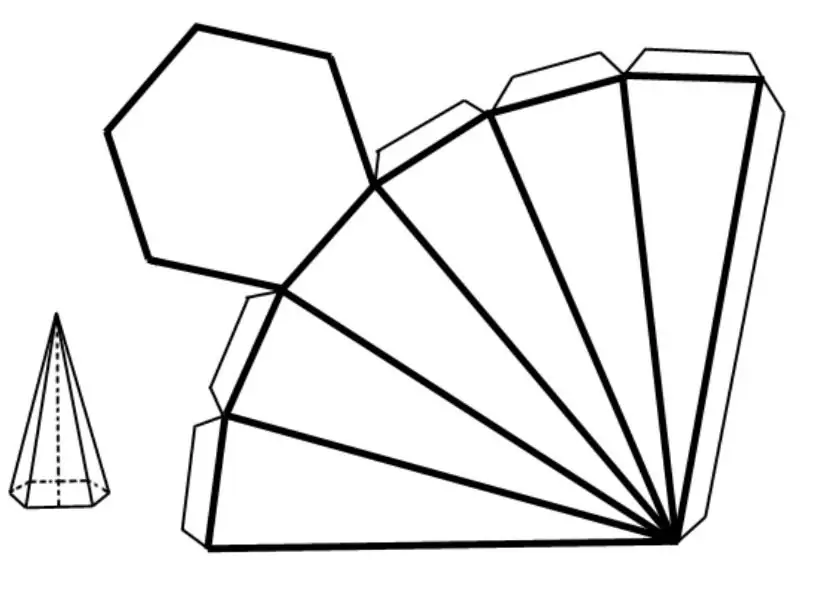
It can be seen that the area of the sweep, and hence the entire surface of the figure under consideration, is equal to the sum of the areas of six identical triangles and one hexagon.
To determine the area of a hexagon S6, use the universal formula for a regular n-gon:
S=n/4a2ctg(pi/n)=>
S6=3√3/2a2.
Where a is the length of the side of the hexagon.
The area of a triangle S3 of the lateral side can be found if you know the value of its height hb:
S3=1/2hba.
Because all sixtriangles are equal to each other, then we get a working expression for determining the area of a hexagonal pyramid with the correct base:
S=S6+ 6S3=3√3/2a2 + 61/2hba=3a(√3/2a + hb).
Pyramid volume
Just like the area, the volume of a hexagonal regular pyramid is its important property. This volume is calculated by the general formula for all pyramids and cones. Let's write it down:
V=1/3Soh.
Here, the symbol So is the area of the hexagonal base, i.e. So=S6.
Substituting the above expression for S6 into the formula for V, we arrive at the final equality for determining the volume of a regular hexagonal pyramid:
V=√3/2a2h.
An example of a geometric problem
In a regular hexagonal pyramid, the lateral edge is twice the length of the base side. Knowing that the latter is 7 cm, it is necessary to calculate the surface area and volume of this figure.
As you might guess, the solution of this problem involves the use of the expressions obtained above for S and V. Nevertheless, it will not be possible to use them right away, since we do not know the apothem and the height of a regular hexagonal pyramid. Let's calculate them.
The apothem hb can be determined by considering a right triangle built on sides b, a/2 and hb. Here b is the length of the side edge. Using the condition of the problem, we get:
hb=√(b2-a2/4)=√(14 2-72/4)=13, 555 cm.
The height h of the pyramid can be determined in exactly the same way as an apothem, but now we should consider a triangle with sides h, b and a, located inside the pyramid. The height will be:
h=√(b2- a2)=√(142- 7 2)=12, 124 cm.
It can be seen that the calculated height value is less than that for the apothem, which is true for any pyramid.
Now you can use expressions for volume and area:
S=3a(√3/2a + hb)=37(√3/27 + 13, 555)=411, 96cm2;
V=√3/2a2h=√3/27212, 124=514, 48cm3.
Thus, to unambiguously determine any characteristic of a regular hexagonal pyramid, you need to know any two of its linear parameters.






