Every schoolchild knows that light in a homogeneous transparent medium moves along a straight path. This fact allows us to consider many optical phenomena within the framework of the concept of a light beam. This article talks about the angle of incidence of the beam, and why it is important to know this angle.
A beam of light is a micrometer electromagnetic wave
In physics, there are waves of various nature: sound, sea, electromagnetic and some others. However, the term "beam" applies only to electromagnetic waves, of which the visible spectrum is a part. The word "ray" itself can be represented as a straight line connecting two points in space.
Light (as a wave) can be seen as a straight line, because each wave implies the presence of vibrations. The answer to this question lies in the value of the wavelength. So, for marine and sound, the length ranges from a few centimeters to tens of meters. Of course, such oscillations can hardly be called a beam. The wavelength of light is less than one micrometer. The human eye is not able to distinguish such vibrations, therefore it seems to us thatthat we see a direct beam.

For the sake of completeness, it should be noted that the light beam is only visible when it begins to scatter on small particles, such as in a dusty room or fog droplets.
Where is it important to know the angle at which the beam hits the obstacle?
The phenomena of reflection and refraction are the most famous optical effects that a person encounters literally every day when he looks at himself in the mirror or drinks a glass of tea after looking at the spoon in it.
The mathematical description of refraction and reflection requires knowledge of the angle of incidence of the beam. For example, the phenomenon of reflection is characterized by the equality of the angle of reflection and incidence. If described from the side of the refraction process, the angle of incidence and the angle of refraction are related to each other through the functions of sines and the refractive indices of the media (Snell's law).

The angle at which a light beam falls on the interface between two transparent media plays an important role when considering the effect of internal total reflection in an optically denser material. This effect is observed only in the case of angles of incidence that are greater than some critical value.
Geometric definition of the considered angle
It can be assumed that there is some surface that separates the two environments. This surface may be flat, as in the case of a mirror, or it may be more complex, such as the ridged surface of the sea. Imagine that on this surface fallslight beam. How to determine the angle of incidence of light? To do this is quite simple. The following is a sequence of actions that should be done to find the desired angle.
- First, you need to determine the point of intersection of the ray with the surface.
- Through O one should draw a perpendicular to the considered surface. It is often called normal.
- The angle of incidence of the beam is equal to the angle between it and the normal. It can be measured with a simple protractor.
As you can see, it is not difficult to find the considered angle. However, students often make the mistake of measuring it between the plane and the beam. It must be remembered that the angle of incidence is always measured from the normal, regardless of the shape of the surface and the medium in which it propagates.
Spherical mirrors, lenses and rays falling on them
Knowledge of the properties of the angles of incidence of certain rays is used in the construction of images in spherical mirrors and thin lenses. To build such images, it is enough to know how two different beams behave when interacting with the named optical devices. The intersection of these rays determines the position of the image point. In the general case, one can always find three different beams, the course of which is exactly known (the third beam can be used to check the correctness of the constructed image). These rays are named below.
- Running parallel to the main optical axis of the device. It passes through the focus after reflection or refraction.
- A beam passing through the focus of the device. It always reflectsrefracted parallel to the principal axis.
- Going through the optical center (for a spherical mirror it coincides with the center of the sphere, for a lens it is inside it). Such a beam does not change its trajectory.
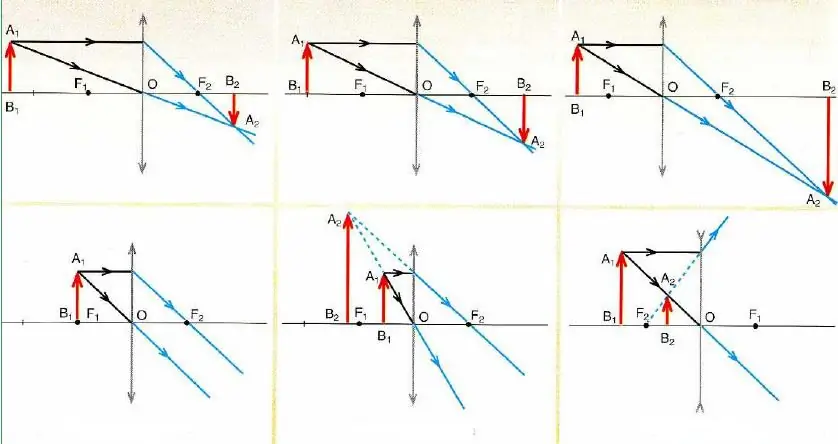
The figure above shows the schemes for constructing images for different options for the location of the object relative to thin lenses.






