Images in lenses, the operation of instruments such as microscopes and telescopes, the rainbow phenomenon and the deceptive perception of the depth of a body of water are all examples of the phenomenon of refraction of light. The laws describing this phenomenon are discussed in this article.
The phenomenon of refraction

Before considering the laws of light refraction in physics, let's get acquainted with the essence of the phenomenon itself.
As you know, if the medium is homogeneous at all points in space, then the light will move in it along a straight path. Refraction of this path occurs when a light beam crosses at an angle the interface between two transparent materials, such as glass and water or air and glass. Moving to another homogeneous medium, the light will also move in a straight line, but it will already be directed at some angle to its trajectory in the first medium. This is the phenomenon of refraction of the light beam.
The video below demonstrates the phenomenon of refraction using glass as an example.

The important point here is the angle of incidence oninterface plane. The value of this angle determines whether the phenomenon of refraction will be observed or not. If the beam falls perpendicularly to the surface, then, having passed into the second medium, it will continue to move along the same straight line. The second case, when refraction will not occur, are the angles of incidence of a beam going from an optically denser medium to a less dense one, which are greater than some critical value. In this case, the light energy will be completely reflected back into the first medium. The last effect is discussed below.
First law of refraction
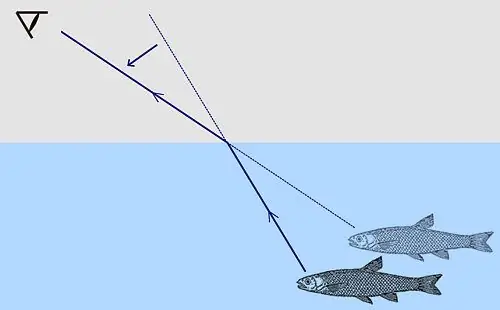
It can also be called the law of three lines in one plane. Suppose there is a beam of light A, which falls on the interface between two transparent materials. At the point O, the beam is refracted and begins to move along the straight line B, which is not a continuation of A. If we restore the perpendicular N to the separation plane to the point O, then the 1st law for the phenomenon of refraction can be formulated as follows: the incident beam A, the normal N and the refracted beam B lie in the same plane, which is perpendicular to the interface plane.
This simple law is not obvious. Its formulation is the result of a generalization of experimental data. Mathematically, it can be derived using the so-called Fermat principle or the principle of least time.
Second law of refraction
School physics teachers often give students the following task: "Formulate the laws of refraction of light." We have considered one of them, now let's move on to the second.
Denote the angle between ray A and perpendicular N as θ1, and the angle between ray B and N as θ2. We also take into account that the speed of beam A in medium 1 is v1, the speed of beam B in medium 2 is v2. Now we can give a mathematical formulation of the 2nd law for the phenomenon under consideration:
sin(θ1)/v1=sin(θ2)/ v2.
This formula was obtained by the Dutchman Snell at the beginning of the 17th century and now bears his last name.
An important conclusion follows from the expression: the greater the speed of light propagation in the medium, the farther from the normal the beam will be (the greater the sine of the angle).
The concept of the refractive index of the medium
The above Snell formula is currently written in a slightly different form, which is more convenient to use when solving practical problems. Indeed, the speed v of light in matter, although less than that in vacuum, is still a large value that is difficult to work with. Therefore, a relative value was introduced into physics, the equality for which is presented below:
n=c/v.
Here c is the speed of the beam in vacuum. The value of n shows how many times the value of c is greater than the value of v in the material. It is called the refractive index of this material.
Taking into account the entered value, the formula of the law of refraction of light will be rewritten in the following form:
sin(θ1)n1=sin(θ2) n2.
Material having a large value of n,called optically dense. Passing through it, light slows down its speed by n times compared to the same value for airless space.
This formula shows that the beam will lie closer to the normal in the medium that is more optically dense.
For example, we note that the refractive index for air is almost equal to one (1, 00029). For water, its value is 1.33.
Total reflection in an optically dense medium
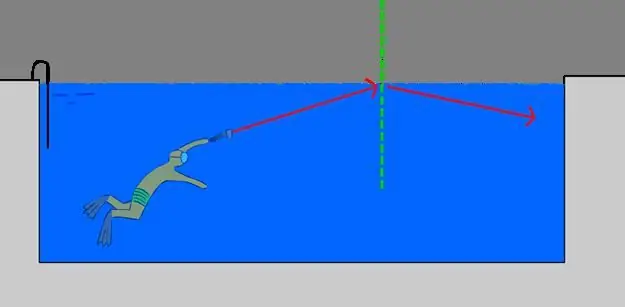
Let's carry out the following experiment: let's start a beam of light from the water column towards its surface. Since water is optically denser than air (1, 33>1, 00029), the angle of incidence θ1 will be less than the angle of refraction θ2. Now, we will gradually increase θ1, respectively, θ2 will also increase, while the inequality θ1 <θ2always stays true.
There will come a moment when θ1<90o and θ2=90 o. This angle θ1 is called critical for a pair of water-air media. Any angles of incidence greater than this will result in no part of the beam passing through the water-air interface into a less dense medium. The entire ray at the boundary will experience total reflection.
Calculation of the critical angle of incidence θc is performed by the formula:
θc=arcsin(n2/n1).
For media water andair it is 48, 77o.
Note that this phenomenon is not reversible, that is, when light moves from air to water, there is no critical angle.

The described phenomenon is used in the operation of optical fibers, and together with the dispersion of light is the cause of the appearance of primary and secondary rainbows during rain.






