The Titius-Bode rule (sometimes simply called Bode's law) is the hypothesis that bodies in some orbital systems, including the Sun, rotate along semi-axes depending on the planetary sequence. The formula suggests that as it extends outward, each planet will be about twice as far from the Sun as the previous one.
The hypothesis correctly predicted the orbits of Ceres (in the asteroid belt) and Uranus, but failed to determine the orbit of Neptune and was eventually replaced by the solar system formation theory. It is named after Johann Daniel Titius and Johann Elert Bode.

Origins
The first mention of a series approximating Bode's law can be found in David Gregory's Elements of Astronomy, published in 1715. In it he says: “… assuming that the distance from the Sun to the Earth is divided into ten equal parts, of which the distance of Mercury will be about four, from Venus seven, from Mars fifteen, from Jupiter fifty-two, and from Saturn ninety-five . A similar suggestion, probably inspired by Gregory, appears in a work published by Christian Wolff in 1724.
In 1764, Charles Bonnet, in his book Contemplation of Nature, said: "We know the seventeen planets that make up our solar system [that is, the main planets and their satellites], but we are not sure that they are no more." To this, in his 1766 translation of Bonnet's work, Johann Daniel Titius added two paragraphs of his own at the bottom of page 7 and at the top of page 8. The new interpolated paragraph is not found in Bonnet's original text: neither in the Italian nor English translations of the work.
Discovery of Titius
There are two parts in the intercalated text of Titius. The first explains the sequence of planetary distances from the Sun. It also contains a few words about the distance from the Sun to Jupiter. But this is not the end of the text.
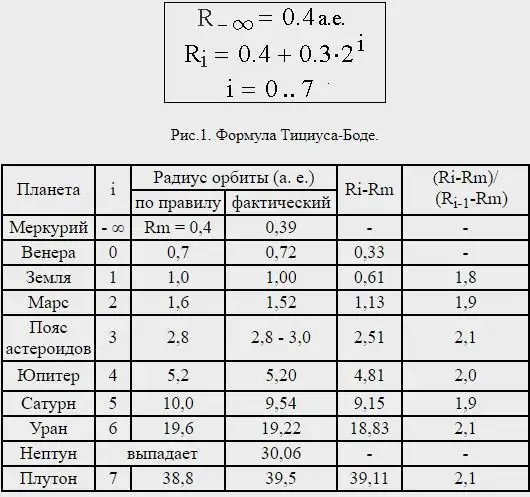
It is worth saying a few words about the formula of the Titius-Bode rule. Pay attention to the distances between the planets and find out that almost all of them are separated from each other in a proportion corresponding to their bodily sizes. Divide the distance from the Sun to Saturn by 100 parts; then Mercury is separated by four such parts from the Sun; Venus - into 4 + 3=7 such parts; Earth - by 4+6=10; Mars - by 4+12=16.
But note that from Mars to Jupiter there is a deviation from this so precise progression. A space of 4 + 24=28 such parts follows from Mars, but so far not a single planet has been discovered there. But should the Lord Architect leave this place empty? Never. Solet's assume that this space belongs without a doubt to the yet undiscovered moons of Mars, and add that perhaps Jupiter still has a few smaller moons around it that have not yet been seen by any telescope.

Rise of the Bode
In 1772, Johann Elert Bode, at the age of twenty-five, completed the second edition of his astronomical compendium Anleitung zur Kenntniss des gestirnten Himmels ("Guide to the knowledge of the starry sky"), to which he added the following footnote, originally unsourced, but noted in later versions. In Bode's memoirs one can find a reference to Titius with a clear recognition of his authority.

Opinion Bode
This is how the Titius-Bode rule in the presentation of the latter sounds: if the distance from the Sun to Saturn is taken equal to 100, then Mercury is separated from the Sun by four such parts. Venus - 4+3=7. Earth - 4+6=10. Mars - 4+12=16.
Now there is a gap in this ordered progression. After Mars there follows a space with a calculation of 4+24=28, in which not a single planet has yet been seen. Can we believe that the Founder of the universe left this space empty? Of course not. From here we come to the distance of Jupiter in the form of calculation 4+48=52 and, finally, to the distance of Saturn - 4+96=100.

These two statements about all specific typology and orbital radii seem to come from ancientastronomy. Many of these theories date back to before the seventeenth century.
Influence
Titius was a student of the German philosopher Christian Freiherr von Wolff (1679-1754). The second part of the inserted text in Bonnet's work is based on von Wolff's 1723 work, Vernünftige Gedanken von den Wirkungen der Natur.
Twentieth century literature assigns the authorship of the Titius-Bode rule to a German philosopher. If so, Titius could learn from him. Another older reference was written by James Gregory in 1702 in his Astronomiae Physicae et geometryae Elementa, where the sequence of planetary distances 4, 7, 10, 16, 52, and 100 became a geometric progression of the ratio 2.
This is Newton's closest formula, and was also found in the writings of Benjamin Martin and Thomas Ceard years before Bonnet's book was published in Germany.
Further work and practical implications
Titius and Bode hoped that the law would lead to the discovery of new planets, and indeed, the discovery of Uranus and Ceres, the distance between which agrees well with the law, contributed to its acceptance by the scientific world.
However, Neptune's distance was very inconsistent, and in fact Pluto - now not considered a planet - is at an average distance that roughly corresponds to the Titius-Bode law predicted for the next planet outside Uranus.
The originally published law was approximately satisfied by all known planets - Mercury and Saturn - with a gap betweenfourth and fifth planets. This was regarded as an interesting, but not of great importance, indicator until the discovery of Uranus in 1781, which fits into the series.
Based on this discovery, Bode called for a search for a fifth planet. Ceres, the largest object in the asteroid belt, was found at Bode's predicted position in 1801. Bode's law was widely accepted until Neptune was discovered in 1846 and shown to be inconsistent with the law.
At the same time, a large number of asteroids discovered in the belt crossed Ceres out of the list of planets. Bode's law was discussed by astronomer and logician Charles Sanders Peirce in 1898 as an example of fallacious reasoning.

Development of the problem
The discovery of Pluto in 1930 further complicated the problem. Even though it didn't match the position predicted by Bode's law, it was about the position the law predicted for Neptune. However, the subsequent discovery of the Kuiper belt, and in particular the object Eris, which is more massive than Pluto but does not conform to Bode's law, further discredited the formula.
Serda's Contribution
The Jesuit Thomas Cerda gave the famous astronomy course in Barcelona in 1760 at the Royal Chair of Mathematics at the College of Sant Jaume de Cordelle (Imperial and Royal Seminary of the Nobles of Cordell). In Cerdas' Tratado, planetary distances appear, obtained by applying Kepler's third law, with an accuracy of 10-3.
If we take as 10 the distance from the Earth andround up to integer, geometric progression [(Dn x 10) - 4] / [(Dn-1 x 10) - 4]=2, from n=2 to n=8, may be expressed. And using a circular uniform fictitious motion to the Kepler anomaly, the Rn values corresponding to the ratios of each planet can be obtained as rn=(Rn - R1) / (Rn-1 - R1), resulting in 1.82; 1, 84; 1, 86; 1.88 and 1.90, where rn=2 - 0.02 (12 - n) is an explicit relation between the Keplerian continuity and the Titius-Bode law, which is considered a random numerical coincidence. The result of the calculation is close to two, but the deuce may well be considered as a rounding of the number 1, 82.

The planet's average speed from n=1 to n=8 reduces distance from the Sun and differs from the uniform decline at n=2 to recover from n=7 (orbital resonance). This affects the distance from the Sun to Jupiter. However, the distance between all other objects within the framework of the notorious rule to which the article is devoted is also determined by this mathematical dynamics.
Theoretical aspect
There is no solid theoretical explanation underlying the Titius-Bode rule, but it is possible that given the combination of orbital resonance and lack of degrees of freedom, any stable planetary system has a high probability of repeating the model described in this theory by the two scientists.
Because this may be a mathematical coincidence rather than a "law of nature", it is sometimes called a rule rather than a "law". However, astrophysicist Alan Boss argues that this is simplycoincidence, and the planetary science journal Icarus is no longer accepting articles attempting to provide improved versions of the "law".
Orbital resonance
Orbital resonance from major orbiting bodies creates regions around the Sun that do not have long-term stable orbits. Planet formation simulation results support the idea that a randomly chosen stable planetary system is likely to satisfy the Titius-Bode rule.

Dubrulle and Graner
Dubrulle and Graner showed that power-law distance rules can be a consequence of models of collapsing clouds of planetary systems that have two symmetries: rotational invariance (the cloud and its contents are axisymmetric) and scale invariance (the cloud and its contents look the same at all scales).
The latter is a feature of many phenomena thought to play a role in planet formation, such as turbulence. The distance from the Sun to the planets of the solar system, proposed by Titius and Bode, was not revised in the framework of the studies of Dubrulle and Graner.






