Formulas for determining the distance from a point to a plane and from a point to a line

2024 Author: Angel Austin | [email protected]. Last modified: 2024-01-02 17:39

Knowing the distance from a point to a plane or to a straight line allows you to calculate the volume and surface area of figures in space. The calculation of this distance in geometry is carried out using the corresponding equations for the specified geometric objects. In the article we will show what formulas can be used to determine it.

Line and plane equations

Before giving formulas for determining the distance from a point to a plane and to a line, let's show what equations describe these objects.

To determine a point, a set of coordinates in the given system of coordinate axes is used. Here we will consider only the Cartesian rectangular system in which the axes have the same unit vectors and are mutually perpendicular. On a plane, an arbitrary point is described by two coordinates, in space - by three.

Different types of equations are used to define a straight line. In accordance with the topic of the article, we presentonly two of them, which are used in two-dimensional space to define lines.

Vector equation. It has the following notation:

(x; y)=(x₀; y_{0) + λ(a; b).}

The first term here represents the coordinates of a known point lying on the line. The second term is the direction vector coordinates multiplied by an arbitrary number λ.

General equation. Its notation is as follows:

Ax + By + C=0;

where A, B, C are some coefficients.

The general equation is more often used to determine lines on a plane, however, to find the distance from a point to a line on a plane, it is more convenient to work with a vector expression.

A plane in three-dimensional space can also be written in several mathematical ways. Nevertheless, most often in problems there is a general equation, which is written as follows:

Ax + By + Cz + D=0.

The advantage of this notation in relation to the others is that it explicitly contains the coordinates of a vector perpendicular to the plane. This vector is called a guide for it, it coincides with the direction of the normal, and its coordinates are equal to (A; B; C).

Note that the above expression coincides with the form of writing a general equation for a straight line in two-dimensional space, so when solving problems, you should be careful not to confuse these geometric objects.

Distance between point and line

Let's show how to calculate the distance between a straight line andpoint in two-dimensional space.

Let there be some point Q(x₁; y_{1) and a line given by the expression:}

(x; y)=(x₀; y_{0) + λ(a; b).}

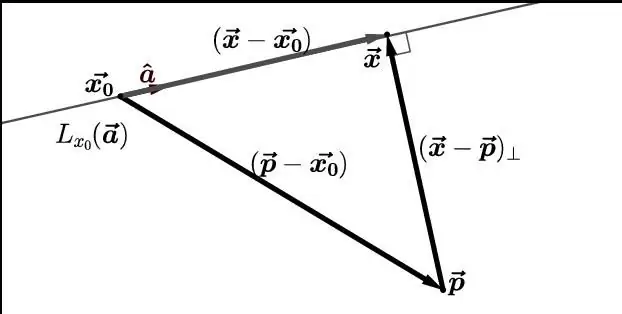
The distance between a line and a point is understood as the length of a segment perpendicular to this line, lowered onto it from the point Q.

Before calculating this distance, you should substitute the Q coordinates into this equation. If they satisfy it, then Q belongs to the given line, and the corresponding distance is equal to zero. If the coordinates of the point do not lead to equality, then the distance between geometric objects is non-zero. It can be calculated using the formula:

d=|[PQ¯u¯]|/|u¯|.

Here P is an arbitrary point of the straight line, which is the beginning of the vector PQ¯. The vector u¯ is a guide segment for a straight line, that is, its coordinates are (a; b).

Using this formula requires the ability to calculate the cross product in the numerator.

Problem with a point and a line

Let's say you need to find the distance between Q(-3; 1) and a straight line that satisfies the equation:

y=5x -2.

Substituting the coordinates of Q into the expression, we can make sure that Q does not lie on the line. You can apply the formula for d given in the paragraph above if you represent this equation in vector form. Let's do it like this:

(x; y)=(x; 5x -2)=>

(x; y)=(x; 5x) + (0; -2)=>

(x; y)=x(1; 5) + (0; -2)=>

(x; y)=(0; -2) + λ(1; 5).

Now let's take any point on this line, for example (0; -2), and build a vector starting at it and ending at Q:

(-3; 1) - (0; -2)=(-3; 3).

Now apply the formula to determine the distance, we get:

d=|[(-3; 3)(1; 5)]|/|(1; 5)|=18/√26 ≈ 3, 53.

Distance from point to plane

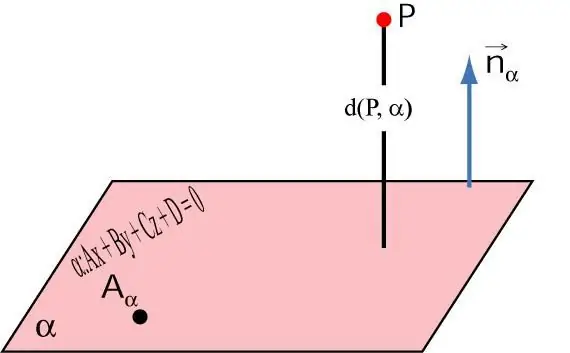
As in the case of a straight line, the distance between a plane and a point in space is understood as the length of the segment, which from a given point is perpendicularly lowered to the plane and intersects it.

In space, a point is given by three coordinates. If they are equal to (x₁; y₁; z_{1), then the distance between the plane and that point can be calculated using the formula:}

d=|Ax₁ + By₁ + Cz₁+ D|/√(A²+B²+C^2).

Note that using the formula allows you to find only the distance from the plane to the line. To find the coordinates of the point at which a perpendicular segment intersects a plane, it is necessary to write an equation for the line to which this segment belongs, and then find a common point for this line and a given plane.

Problem with a plane and a point

Find the distance from a point to a plane if it is known that the point has coordinates (3; -1; 2) and the plane is given by:

-y + 3z=0.

To use the corresponding formula, we first write out the coefficients forgiven plane. Since the variable x and the free term are absent, the coefficients A and D are equal to zero. We have:

A=0; B=-1; C=3; D=0.

It is easy to show that this plane passes through the origin and the x-axis belongs to it.

Substitute the coordinates of the point and the coefficients of the plane into the formula for the distance d, we get:

d=|03 + (-1)(-1) + 23 + 0|/√(1 +9)=7/√10 ≈ 2, 21.

Note that if you change the x-coordinate of a point, then the distance d will not change. This fact means that the set of points (x; -1; 2) forms a straight line parallel to the given plane.