Vector is an important geometric object, with the help of its properties it is convenient to solve many problems on the plane and in space. In this article, we will define it, consider its main characteristics, and also show how a vector in space can be used to define planes.
What is a vector: two-dimensional case
First of all, it is necessary to clearly understand what object we are talking about. In geometry, a directed segment is called a vector. Like any segment, it is characterized by two main elements: the start and end points. The coordinates of these points uniquely determine all the characteristics of the vector.
Let's consider an example of a vector on a plane. To do this, we draw two mutually perpendicular axes x and y. Let us mark an arbitrary point P(x, y). If we connect this point to the origin (point O), and then specify the direction to P, then we get the vector OP¯ (later in the article, the bar over the symbol indicates that we are considering a vector). The vector drawing on the plane is shown below.
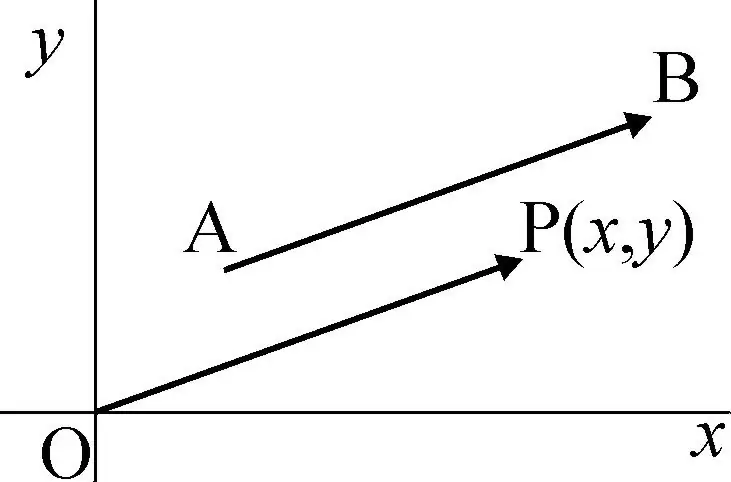
Here, another vector AB¯ is also shown, and you can see that its characteristics are exactly the same as OP¯, but it is in a different part of the coordinate system. By parallel translation OP¯, you can get an infinite number of vectors with the same properties.
Vector in space
All real objects that surround us are in three-dimensional space. The study of the geometric properties of three-dimensional figures deals with stereometry, which operates with the concept of three-dimensional vectors. They differ from two-dimensional ones only in that their description requires an additional coordinate, which is measured along the third perpendicular x and y axis z.
The figure below shows a vector in space. The coordinates of its end along each axis are indicated by colored segments. The beginning of the vector is located at the intersection point of all three coordinate axes, that is, it has coordinates (0; 0; 0).
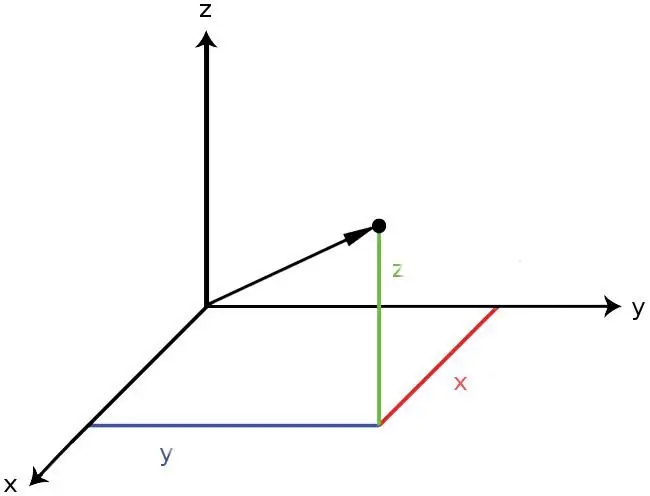
Since a vector on a plane is a special case of a spatially directed segment, then in the article we will consider only a three-dimensional vector.
Vector coordinates based on known coordinates of its start and end
Suppose there are two points P(x1; y1; z1) and Q(x2; y2; z2). How to determine the coordinates of the vector PQ¯. First, it is necessary to agree which of the points will be the beginning and which the end of the vector. In mathematics, it is customary to write the object in question along its direction, that is, P is the beginning, Q- the end. Secondly, the coordinates of the vector PQ¯ are calculated as the difference between the corresponding coordinates of the end and the beginning, that is:
PQ¯=(x2- x1; y2- y 1; z2- z1).
Note that by changing the direction of the vector, its coordinates will change sign, as follows:
QP¯=(x1- x2; y1- y 2; z1- z2).
This means PQ¯=-QP¯.
It is important to understand one more thing. It was said above that in the plane there are an infinite number of vectors equal to the given one. This fact is also valid for the spatial case. In fact, when we calculated the coordinates of PQ¯ in the example above, we carried out the operation of parallel translation of this vector in such a way that its origin coincided with the origin. Vector PQ¯ can be drawn as a directed segment from the origin to point M((x2 - x1; y2 - y1; z2 - z1).
Vector properties
Like any geometry object, a vector has some inherent characteristics that can be used to solve problems. Let's briefly list them.
Vector modulus is the length of the directed segment. Knowing the coordinates, it is easy to calculate it. For the vector PQ¯ in the example above, the modulus is:
|PQ¯|=√[(x2- x1)2 + (y2 - y1)2+ (z2 - z1 )2].
Vector module onplane is calculated by a similar formula, only without the participation of the third coordinate.
The sum and difference of vectors is carried out according to the triangle rule. The figure below shows how to add and subtract these objects.

To get the sum vector, add the beginning of the second to the end of the first vector. The desired vector will start at the beginning of the first and end at the end of the second vector.
The difference is performed taking into account the fact that the subtracted vector is replaced by the opposite one, and then the addition operation described above is performed.
Besides addition and subtraction, it is important to be able to multiply a vector by a number. If the number is equal to k, then a vector is obtained whose modulus is k times different from the original one, and the direction is either the same (k>0) or opposite to the original one (k<0).
The operation of multiplication of vectors among themselves is also defined. We will single out a separate paragraph for it in the article.
Scalar and vector multiplication
Suppose there are two vectors u¯(x1; y1; z1) and v¯(x2; y2; z2). Vector by vector can be multiplied in two different ways:
- Scalar. In this case, the result is a number.
- Vector. The result is some new vector.
The scalar product of vectors u¯ and v¯ is calculated as follows:
(u¯v¯)=|u¯||v¯|cos(α).
Where α is the angle between the given vectors.
It can be shown that knowing the coordinates u¯ and v¯, their dot product can be calculated using the following formula:
(u¯v¯)=x1x2+ y1 y2+ z1z2.
The scalar product is convenient to use when decomposing a vector into two perpendicularly directed segments. It is also used to calculate the parallelism or orthogonality of vectors, and to calculate the angle between them.
The cross product of u¯ and v¯ gives a new vector that is perpendicular to the original ones and has modulus:
[u¯v¯]=|u¯||v¯|sin(α).
Direction down or up of the new vector is determined by the rule of the right hand (four fingers of the right hand are directed from the end of the first vector to the end of the second, and the thumb sticking up indicates the direction of the new vector). The figure below shows the result of the cross product for arbitrary a¯ and b¯.
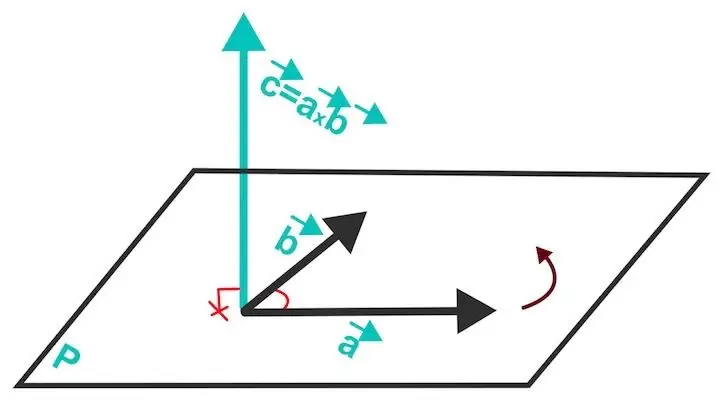
The cross product is used to calculate the areas of figures, as well as to determine the coordinates of a vector perpendicular to a given plane.
Vectors and their properties are convenient to use when defining the equation of a plane.
Normal and general equation of the plane
There are several ways to define a plane. One of them is the derivation of the general equation of the plane, which follows directly from the knowledge of the vector perpendicular to it and some known point that belongs to the plane.
Suppose there is a vector n¯ (A; B; C) and a point P (x0; y0; z 0). What condition will satisfy all points Q(x; y; z) of the plane? This condition consists in the perpendicularity of any vector PQ¯ to the normal n¯. For two perpendicular vectors, the dot product becomes zero (cos(90o)=0), write this:
(n¯PQ¯)=0 or
A(x-x0)+B(y-y0)+C(z-z0)=0.
Opening the brackets, we get:
Ax + By + Cz + (-Ax0-By0-C z0)=0 or
Ax + By + Cz +D=0 where D=-Ax0-By0 -Cz0.
This equation is called general for the plane. We see that the coefficients in front of x, y, and z are the coordinates of the perpendicular vector n¯. It's called a plane guide.
Vector parametric equation of the plane
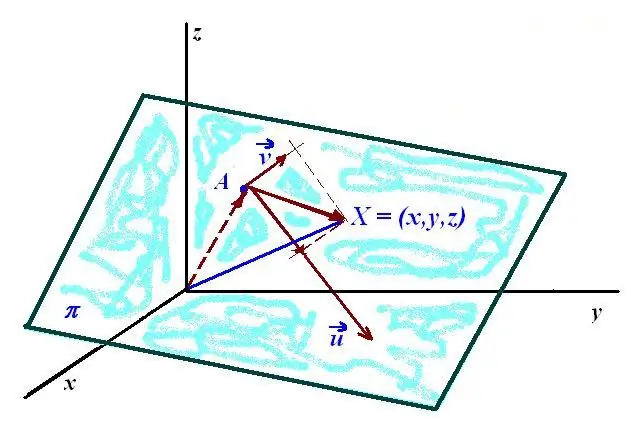
The second way to define a plane is to use two vectors lying in it.
Assume that there are vectors u¯(x1; y1; z1) and v¯(x2; y2; z2). As it was said, each of them in space can be represented by an infinite number of identical directed segments, therefore, one more point is needed to uniquely determine the plane. Let this point be P(x0;y0; z0). Any point Q(x; y; z) will lie in the desired plane if the vector PQ¯ can be represented as a combination of u¯ and v¯. That is, we have:
PQ¯=αu¯ + βv¯.
Where α and β are some real numbers. From this equality follows the expression:
(x; y; z)=(x0; y0; z0) + α(x1; y1; z1) + β(x 2; y2; z2).
It is called a parametric vector equation of the plane with respect to 2 vectors u¯ and v¯. Substituting arbitrary parameters α and β, one can find all points (x; y; z) belonging to this plane.
From this equation it is easy to get the general expression for the plane. To do this, it is enough to find a direction vector n¯ that will be perpendicular to both vectors u¯ and v¯, that is, their vector product should be applied.
The problem of determining the general equation of the plane
Let's show how to use the above formulas to solve geometric problems. Suppose the direction vector of the plane is n¯(5; -3; 1). You should find the equation of the plane, knowing that the point P(2; 0; 0) belongs to it.
The general equation is written as:
Ax + By + Cz +D=0.
Since the vector perpendicular to the plane is known, the equation will take the form:
5x - 3y + z +D=0.
It remains to find the free term D. We calculate it from the knowledge of the coordinates P:
D=-Ax0-By0-Cz0=-52 + 30 - 10=-10.
Thus, the desired equation of the plane has the form:
5x - 3y + z -10=0.
The figure below shows what the resulting plane looks like.

The indicated coordinates of the points correspond to the intersections of the plane with the x, y and z axes.
The problem of determining the plane through two vectors and a point
Now suppose the previous plane is defined differently. Two vectors u¯(-2; 0; 10) and v¯(-2; -10/3; 0) are known, as well as the point P(2; 0; 0). How to write the plane equation in vector parametric form? Using the considered corresponding formula, we get:
(x; y; z)=(2; 0; 0) + α(-2; 0; 10) + β(-2; -10/3; 0).
Note that the definitions of this equation of the plane, the vectors u¯ and v¯ can be taken absolutely any, but with one condition: they must not be parallel. Otherwise, the plane cannot be uniquely determined, however, one can find an equation for a beam or a set of planes.






