Hexagonal prism and its main characteristics

2024 Author: Angel Austin | [email protected]. Last modified: 2024-01-02 17:39

Spatial geometry is the study of prisms. Their important characteristics are the volume contained in them, the surface area and the number of constituent elements. In the article, we will consider all these properties for a hexagonal prism.

Which prism are we talking about?

A hexagonal prism is a figure formed by two polygons with six sides and six angles, and six parallelograms connecting the marked hexagons into a single geometric formation.

The figure shows an example of this prism.

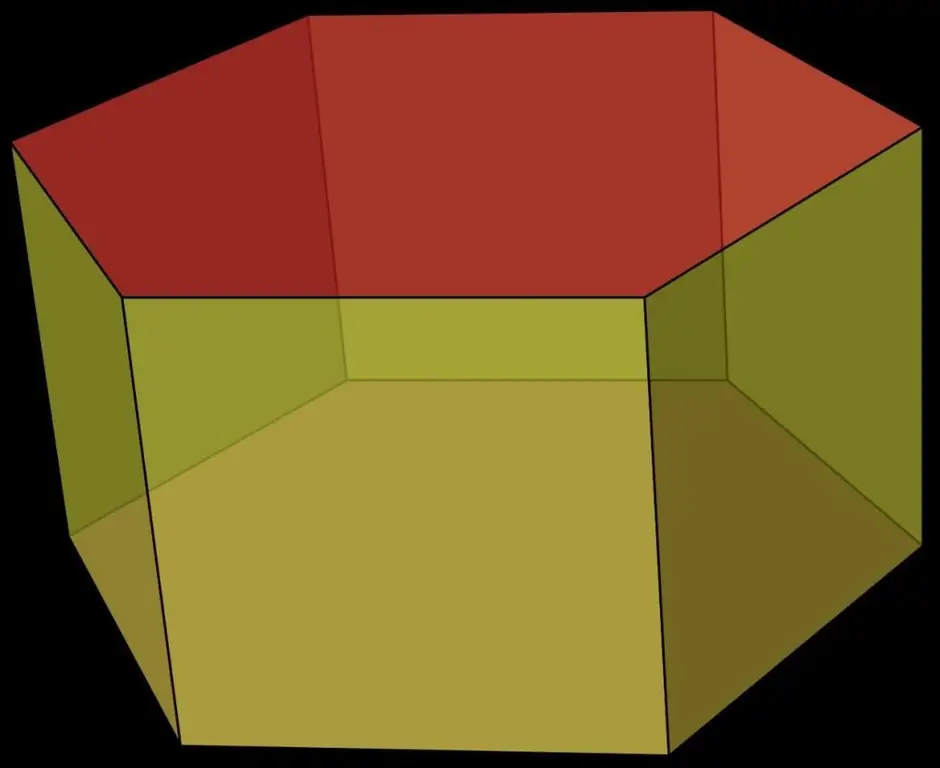
The hexagon marked in red is called the base of the figure. Obviously, the number of its bases is equal to two, and both of them are identical. The yellow-greenish faces of a prism are called its sides. In the figure they are represented by squares, but in general they are parallelograms.

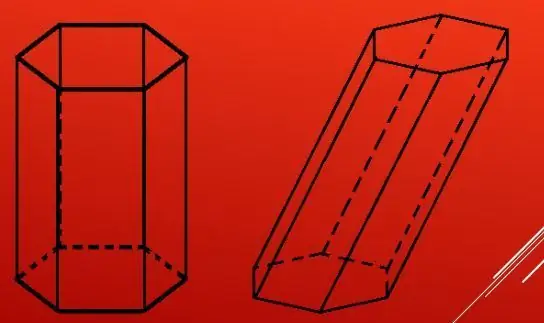
The hexagonal prism can be inclined and straight. In the first case, the angles between the base and the sides are not straight, in the second they are equal to 90o. Also, this prism can be correct and incorrect. Regular hexagon althe prism must be straight and have a regular hexagon at the base. The above prism in the figure satisfies these requirements, so it is called correct. Further in the article we will study only its properties, as a general case.

Elements

For any prism its main elements are edges, faces and vertices. The hexagonal prism is no exception. The figure above allows you to count the number of these elements. So, we get 8 faces or sides (two bases and six lateral parallelograms), the number of vertices is 12 (6 vertices for each base), the number of edges of a hexagonal prism is 18 (six lateral and 12 for the bases).

In the 1750s, Leonhard Euler (a Swiss mathematician) established for all polyhedra, which include a prism, a mathematical relationship between the numbers of the indicated elements. This relationship looks like:

number of edges=number of faces + number of vertices - 2.

The above figures satisfy this formula.

Prism diagonals

All diagonals of a hexagonal prism can be divided into two types:

• those that lie in the planes of its faces;
• those that belong to the entire volume of the figure.

The picture below shows all these diagonals.

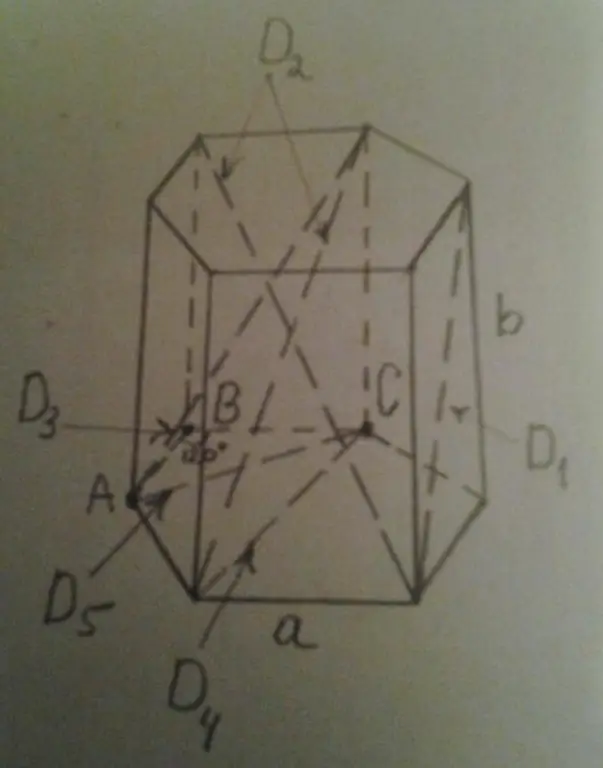
It can be seen that D₁ is the side diagonal, D₂ and D₃ are the diagonals the entire prism, D₄ and D_{5 - the diagonals of the base.}

The lengths of the diagonals of the sides are equal to each other. It is easy to calculate them using the well-known Pythagorean theorem. Let us denote the length of the side of the hexagon by the symbol a, the length of the side edge by the symbol b. Then the diagonal has length:

D₁=√(a² + b^2).

Diagonal D₄ is also easy to determine. If we recall that a regular hexagon fits into a circle with radius a, then D_{4 is the diameter of this circle, that is, we get the following formula:}

D_4=2a.

Diagonal D₅bases are somewhat harder to find. To do this, consider an equilateral triangle ABC (see Fig.). For him AB=BC=a, the angle ABC is 120^{o. If we lower the height from this angle (it will also be the bisector and median), then half of the AC base will be equal to:}

AC/2=ABsin(60o)=a√3/2.

The AC side is the diagonal of D_{5, so we get:}

D_5=AC=√3a.

Now it remains to find the diagonals D₂and D_{3of a regular hexagonal prism. To do this, you need to see that they are the hypotenuses of the corresponding right triangles. Using the Pythagorean theorem, we get:}

D₂=√(D₄²+ b^2)=√(4a2^{+ b}2^);

D₃=√(D₅²+ b^2)=√(3a2^{+ b}2^).

Thus, the largest diagonal for any values of a and b isD_2.

Surface area

To understand what is at stake, the easiest way is to consider the development of this prism. It is shown in the picture.

It can be seen that to determine the area of all sides of the figure under consideration, it is necessary to calculate the area of the quadrangle and the area of the hexagon separately, then multiply them by the corresponding integers equal to the number of each n-gon in the prism, and add the results. Hexagons 2, rectangles 6.

For the area of a rectangle we get:

S_1=ab.

Then the lateral surface area is:

S_2=6ab.

To determine the area of a hexagon, the easiest way is to use the corresponding formula, which looks like:

S=n/4a2ctg(pi/n).

Substituting the number n equal to 6 into this expression, we get the area of one hexagon:

S₆=6/4a²ctg(pi/6)=3√3/2a 2^.

This expression should be multiplied by two to get the area of the bases of the prism:

S_os=3√3a^2.

It remains to add S_os and S_{2 to get the total surface area of the figure:}

S=S_os+ S₂=3√3a^{2+ 6ab=3a(√3a + 2b).}

Prism volume

After the formula forarea of a hexagonal base, calculating the volume contained in the prism in question is as easy as shelling pears. To do this, you just need to multiply the area of \u200b\u200bone base (hexagon) by the height of the figure, the length of which is equal to the length of the side edge. We get the formula:

V=S₆b=3√3/2a^2b.

Note that the product of the base and the height gives the value of the volume of absolutely any prism, including the oblique one. However, in the latter case, the calculation of the height is complicated, since it will no longer be equal to the length of the side rib. As for a regular hexagonal prism, the value of its volume is a function of two variables: sides a and b.