Of the many geometric shapes, one of the simplest can be called a parallelepiped. It has the shape of a prism, at the base of which is a parallelogram. It is not difficult to calculate the area of the box because the formula is very simple.
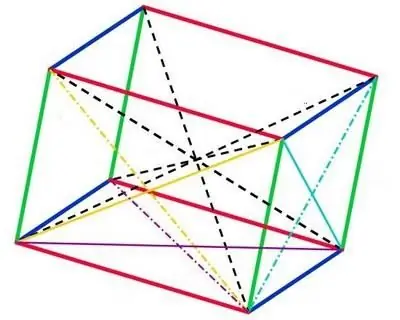
A prism consists of faces, vertices and edges. The distribution of these constituent elements is made in the minimum amount that is necessary to form this geometric shape. The parallelepiped contains 6 faces, which are connected by 8 vertices and 12 edges. Moreover, the opposite sides of the parallelepiped will always be equal to each other. Therefore, to find out the area of a parallelepiped, it is enough to determine the dimensions of its three faces.
The parallelepiped (Greek for "parallel edges") has some properties worth mentioning. Firstly, the symmetry of the figure is confirmed only in the middle of each of its diagonals. Secondly, by drawing a diagonal between any of the opposite vertices, you can find that all vertices have a single pointintersections. It is also worth noting the property that opposite faces are always equal and will necessarily be parallel to each other.
In nature, these types of parallelepipeds are distinguished:
- rectangular - consists of rectangular faces;
- straight - has only rectangular side faces;
- an inclined parallelepiped has side faces that are not perpendicular to the bases;
- cube - consists of square-shaped faces.
Let's try to find the area of a parallelepiped using the rectangular type of this figure as an example. As we already know, all its faces are rectangular. And since the number of these elements is reduced to six, then, having learned the area of \u200b\u200beach face, it is necessary to summarize the results obtained into one number. And to find the area of each of them is not difficult. To do this, multiply the two sides of the rectangle.
Use a mathematical formula to determine the area of a cuboid. It consists of symbolic symbols denoting faces, area, and looks like this: S=2(ab+bc+ac), where S is the area of the figure, a, b are the sides of the base, c is the side edge.
Let's give an example calculation. Let's say a \u003d 20 cm, b \u003d 16 cm, c \u003d 10 cm. Now you need to multiply the numbers in accordance with the requirements of the formula: 2016 + 1610 + 2010 and we get the number 680 cm2. But this will be only half of the figure, since we have learned and summarized the areas of three faces. Because each edge hasits "double", you need to double the resulting value, and we get the area of the parallelepiped, equal to 1360 cm2.
To calculate the lateral surface area, apply the formula S=2c(a+b). The area of the base of a parallelepiped can be found by multiplying the lengths of the sides of the base by each other.

In everyday life, parallelepipeds can often be found. We are reminded of their existence by the shape of a brick, a wooden desk box, or an ordinary matchbox. Examples can be found in abundance around us. In school curricula on geometry, several lessons are devoted to the study of a parallelepiped. The first of them demonstrate models of a rectangular parallelepiped. Then the students are shown how to inscribe a ball or pyramid, other figures into it, find the area of the parallelepiped. In a word, this is the simplest three-dimensional figure.






