What are variables? Variable in mathematics

2024 Author: Angel Austin | [email protected]. Last modified: 2024-01-02 17:39

The importance of variables in mathematics is great, because during its existence, scientists managed to make many discoveries in this area, and in order to briefly and clearly state this or that theorem, we use variables to write the corresponding formulas. For example, the Pythagorean theorem on a right triangle: a² =b² + c^{2. How to write every time when solving a problem: according to the Pythagorean theorem, the square of the hypotenuse is equal to the sum of the squares of the legs - we write this down with a formula, and everything immediately becomes clear.}

So, this article will discuss what variables are, their types and properties. Various mathematical expressions will also be considered: inequalities, formulas, systems and algorithms for their solution.

Variable concept

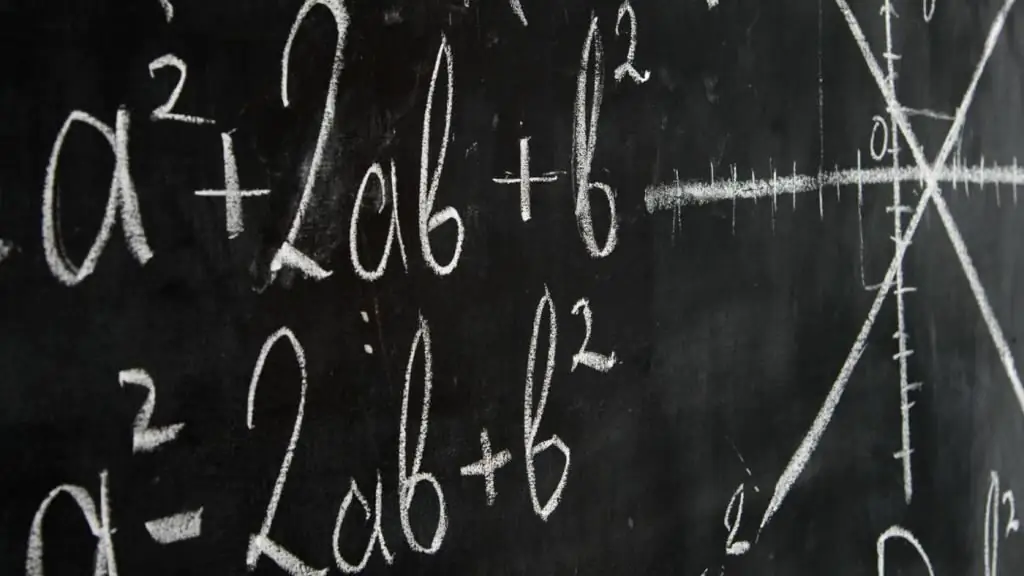
First of all, what is a variable? This is a numerical value that can take on many values. It cannot be constant, since in different problems and equations, for convenience, we take solutions asvariable different numbers, that is, for example, z is a general designation for each of the quantities for which it is taken. Usually they are denoted by letters of the Latin or Greek alphabet (x, y, a, b, and so on).

There are different kinds of variables. They set both some physical quantities - path (S), time (t), and simply unknown values in equations, functions and other expressions.

For example, there is a formula: S=Vt. Here, the variables denote certain quantities related to the real world - the path, speed and time.

And there is an equation of the form: 3x - 16=12x. Here, x is already taken as an abstract number that makes sense in this notation.

Types of quantities

Amount means something that expresses the properties of a certain object, substance or phenomenon. For example, air temperature, weight of an animal, percentage of vitamins in a tablet - these are all quantities whose numerical values can be calculated.

Each quantity has its own units of measurement, which together form a system. It is called the number system (SI).

What are variables and constants? Consider them with specific examples.

Let's take rectilinear uniform motion. A point in space moves at the same speed every time. That is, time and distance change, but the speed remains the same. In this example, time and distance are variables, and speed is constant.

Or, for example, “pi”. This is an irrational number that continues without repeatinga sequence of digits and cannot be written in full, so in mathematics it is expressed by a generally accepted symbol that takes only the value of a given infinite fraction. That is, “pi” is a constant value.

History

The history of the notation of variables begins in the seventeenth century with the scientist René Descartes.

He designated the known values with the first letters of the alphabet: a, b and so on, and for the unknown he suggested using the last letters: x, y, z. It is noteworthy that Descartes considered such variables to be non-negative numbers, and when faced with negative parameters, he put a minus sign in front of the variable or, if it was not known what sign the number was, an ellipsis. But over time, the names of variables began to denote numbers of any sign, and this began with the mathematician Johann Hudde.

With variables, calculations in mathematics are easier to solve, because, for example, how do we now solve biquadratic equations? We enter a variable. For example:

x⁴ + 15x^{2 + 7=0}

For x2 we take some k, and the equation becomes clear:

x2=k, for k ≧ 0

k2 + 15k + 7=0

That's what the introduction of variables brings to mathematics.

Inequalities, examples of solutions

An inequality is a record in which two mathematical expressions or two numbers are connected by comparison signs:, ≦, ≧. They are strict and are indicated by signs or non-strict with signs ≦, ≧.

For the first time these signs introducedThomas Harriot. After Thomas's death, his book with these notations was published, mathematicians liked them, and over time they became widely used in mathematical calculations.

There are several rules to follow when solving single variable inequalities:

When transferring a number from one part of the inequality to another, change its sign to the opposite.
When multiplying or dividing parts of an inequality by a negative number, their signs are reversed.
If you multiply or divide both sides of the inequality by a positive number, you get an inequality equal to the original one.

Solving an inequality means finding all valid values for a variable.

Single variable example:

10x - 50 > 150

We solve it like a normal linear equation - we move the terms with a variable to the left, without a variable - to the right and give similar terms:

10x > 200

We divide both sides of the inequality by 10 and get:

x > 20

For clarity, in the example of solving an inequality with one variable, draw a number line, mark the pierced point 20 on it, since the inequality is strict, and this number is not included in the set of its solutions.

The solution to this inequality is the interval (20; +∞).

Solution of a non-strict inequality is carried out in the same way as a strict one:

6x - 12 ≧ 18

6x ≧ 30

x ≧ 5

But there is one exception. A record of the form x ≧ 5 should be understood as follows: x is greater than or equal to five, which meansthe number five is included in the set of all solutions to the inequality, that is, when writing the answer, we put a square bracket in front of the number five.

x ∈ [5; +∞)

Square inequalities

If we take a quadratic equation of the form ax2 + bx +c=0 and change the equal sign to the inequality sign in it, then we will accordingly obtain a quadratic inequality.

To solve a quadratic inequality, you need to be able to solve quadratic equations.

y=ax2 + bx + c is a quadratic function. We can solve it using the discriminant, or using the Vieta theorem. Recall how these equations are solved:

1) y=x2 + 12x + 11 - the function is a parabola. Its branches are directed upwards, since the sign of the coefficient "a" is positive.

2) x2 + 12x + 11=0 - equate to zero and solve using the discriminant.

a=1, b=12, c=11

D=b2 - 4ac=144 - 44=100 > 0, 2 roots

According to the formula of the roots of the quadratic equation, we get:

x₁ =-1, x_2=-11

Or you could solve this equation using the Vieta theorem:

x₁ + x₂ =-b/a, x₁ + x _2=-12

x₁x₂ =c/a, x₁x₂₌₁₁

Using the selection method, we obtain the same roots of the equation.

Parabola

So, the first way to solve a quadratic inequality is a parabola. The algorithm for solving it is as follows:

1. Determine where the branches of the parabola are directed.

2. Equate the function to zero and find the roots of the equation.

3. We build a number line, mark the roots on it, draw a parabola and find the gap we need, depending on the sign of the inequality.

Solve the inequality x2 + x - 12 > 0

Write out as a function:

1) y=x2 + x - 12 - parabola, branches up.

Set to zero.

2) x2 + x -12=0

Next, we solve as a quadratic equation and find the zeros of the function:

x₁ =3, x_2=-4

3) Draw a number line with points 3 and -4 on it. The parabola will pass through them, branches up and the answer to the inequality will be a set of positive values, that is, (-∞; -4), (3; +∞).

Interval method

The second way is the spacing method. Algorithm for solving it:

1. Find the roots of the equation for which the inequality is equal to zero.

2. We mark them on the number line. Thus, it is divided into several intervals.

3. Determine the sign of any interval.

4. We place signs at the remaining intervals, changing them after one.

Solve the inequality (x - 4)(x - 5)(x + 7) ≦ 0

1) Inequality zeros: 4, 5 and -7.

2) Draw them on the number line.

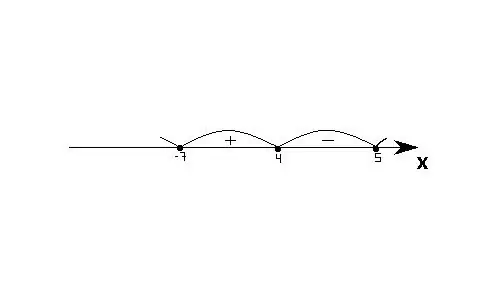
3) Determine the signs of intervals.

Answer: (-∞; -7]; [4; 5].

Solve one more inequality: x2(3x - 6)(x + 2)(x - 1) > 0

1. Inequality zeros: 0, 2, -2 and 1.

2. Mark them on the number line.

3. Determine interval signs.

The line is divided into intervals - from -2 to 0, from 0 to 1, from 1 to 2.

Take the value on the first interval - (-1). Substitute in inequality. With this value, the inequality becomes positive, which means that the sign on this interval will be +.

Further, starting from the first gap, we arrange the signs, changing them after one.

The inequality is greater than zero, that is, you need to find a set of positive values on the line.

Answer: (-2; 0), (1; 2).

Systems of equations

A system of equations with two variables is two equations joined by a curly brace for which it is necessary to find a common solution.

Systems can be equivalent if the general solution of one of them is the solution of the other, or both of them have no solutions.

We will study the solution of systems of equations with two variables. There are two ways to solve them - the substitution method or the algebraic method.

Algebraic method

To solve the system shown in the picture using this method, you must first multiply one of its parts by such a number, so that later you can mutually cancel one variable from both parts of the equation. Here we multiply by three, draw a line under the system and add up its parts. As a result, x's become identical in modulus, but opposite in sign, and we reduce them. Next, we get a linear equation with one variable and solve it.

We found Y, but we can't stop there, because we haven't found X yet. SubstituteY to the part from which it will be convenient to withdraw X, for example:

-x + 5y=8, with y=1

-x + 5=8

Solve the resulting equation and find x.

-x=-5 + 8

-x=3

x=-3

The main thing in the solution of the system is to write down the answer correctly. Many students make the mistake of writing:

Answer: -3, 1.

But this is a wrong entry. After all, as already mentioned above, when solving a system of equations, we are looking for a general solution for its parts. The correct answer would be:

(-3; 1)