Finding the area of a trapezoid is one of the basic actions that allows you to solve many geometry problems. Also in KIM in mathematics of the OGE and the Unified State Examination there are many tasks for which you need to know how to find the area of \u200b\u200bthis geometric figure. This article will cover all formulas for the area of a trapezoid.
What is this figure?

Before considering all the formulas for the area of a trapezoid, you need to know what it is, because without a clear definition it is impossible to correctly use the formulas and properties of this figure. A trapezoid is a quadrilateral whose two sides are opposite each other, and if you continue them to infinite lines, then they will never intersect (these sides are the bases of the figure). The other two sides can have obtuse and acute angles and are called lateral (at the same time, if its sides are the same, and the angles at the base are pairwise equal to each other, then such a trapezoid is calledequilateral). All formulas for the area of this quadrilateral are discussed below.
All formulas for the area of a trapezoid
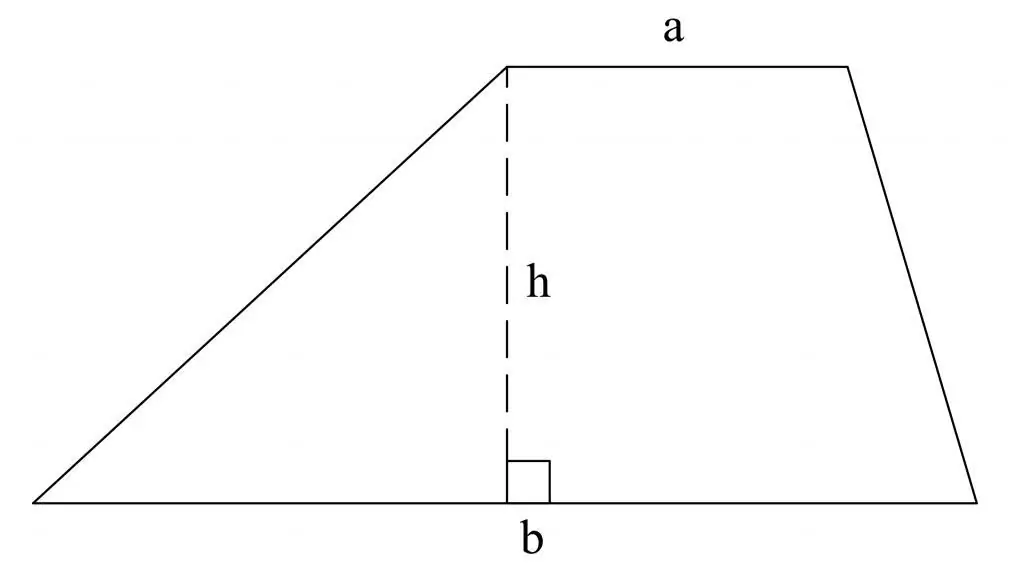
In geometry, there are many formulas for finding the areas of figures, which is both a plus and a minus. How to find the area of a trapezoid?
- Through diagonals and vertical angle. To do this, multiply half the product of the diagonals by the angle between them.
- Trapezoid area through base and height. Multiply half the sum of the bases by the height of the trapezoid drawn to one of the bases.
- With the help of all sides. Divide the sum of the bases in half and multiply by the root. Under the root: side squared minus a fraction whose numerator is the difference of the bases squared plus the difference of the sides, each of which is squared, and the denominator is the difference of the bases multiplied by two.
- Through height and median. Divide the sum of the bases of the trapezoid in half and multiply by the height drawn to the base of the figure.
- For an isosceles trapezoid there is also a formula for finding the area. To find the area of this figure, multiply the square of the radius by four and divide by the sine of the angle alpha.
Properties of the bisector of a trapezoid
Like the bisector of an isosceles triangle drawn to the base, a straight line dividing the angle in half, this figure has its own properties that are useful when solving problems in geometry.
- Bisectors with sides not parallel to each other,are perpendiculars (from this property it follows that they form a right triangle, the hypotenuse of which is the lateral side of this figure).
- The point of their intersection at the side that is the base of this figure belongs to another base (it follows from this property that an isosceles triangle is formed at the base with such right obtuse angles).
- The bisector cuts off from the base a segment of the same length as the side (from this property it follows that it forms an isosceles triangle with the base, the side and the base of the trapezoid will be the sides, and the bisector will be the base of an isosceles triangle).
Conclusion
In this article, all the formulas for the area of a trapezoid were proposed. Most of them are not covered in geometry textbooks, but they are all necessary for successful problem solving.






