Triangle is a two-dimensional figure with three edges and the same number of vertices. It is one of the basic shapes in geometry. An object has three angles, their total degree measure is always 180°. Vertices are usually denoted by Latin letters, for example, ABC.
Theory
Triangles can be classified according to different criteria.
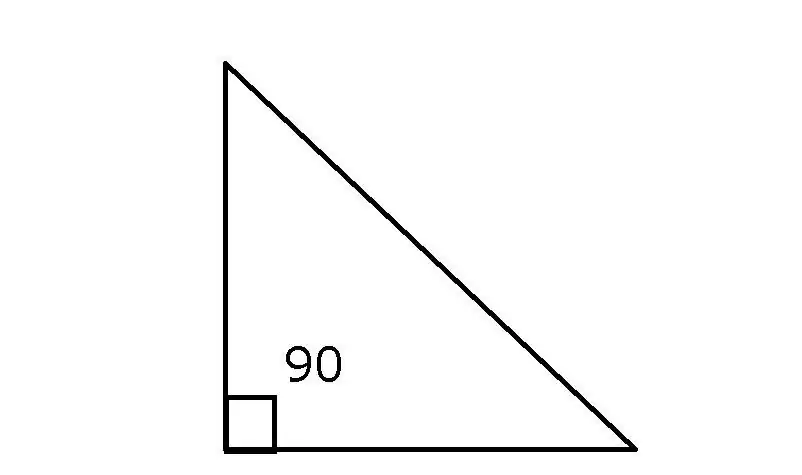
If the degree measure of all its angles is less than 90 degrees, then it is called acute-angled, if one of them is equal to this value - rectangular, and in other cases - obtuse-angled.
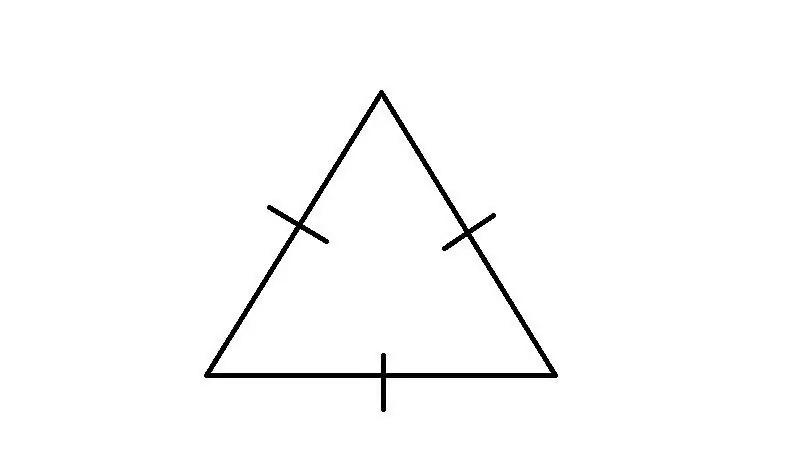
When a triangle has all sides of the same size, it is called equilateral. In the figure, this is marked with a mark perpendicular to the segment. Angles in in this case are always 60°.
If only two sides of a triangle are equal, then it is called isosceles. In this case, the angles at the base are equal.
A triangle that does not fit the two previous options is called scalene.
When two triangles are said to be equal, it means they are the same sizeand form. They also have the same angles.
If only degree measures coincide, then the figures are called similar. Then the ratio of the corresponding sides can be expressed by a certain number, which is called the coefficient of proportionality.
Perimeter of a triangle in terms of area or sides
As with any polygon, the perimeter is the sum of the lengths of all sides.
For a triangle, the formula looks like this: P=a + b + c, where a, b and c are the lengths of the sides.
There is another way to solve this problem. It consists in finding the perimeter of a triangle through the area. First you need to know the equation that relates these two quantities.
S=p × r, where p is the semiperimeter and r is the radius of the circle inscribed in the object.
It is quite easy to transform the equation into the form we need. Get:
p=S/r
Do not forget that the real perimeter will be 2 times larger than the received one.
P=2S/r
This is how simple examples like this are solved.






