Six important phenomena describe the behavior of a light wave if it encounters an obstacle in its path. These phenomena include reflection, refraction, polarization, dispersion, interference and diffraction of light. This article will focus on the last of them.
Disputes about the nature of light and the experiments of Thomas Young
In the middle of the 17th century, there were two theories on equal terms regarding the nature of light rays. The founder of one of them was Isaac Newton, who believed that light is a collection of rapidly moving particles of matter. The second theory was put forward by the Dutch scientist Christian Huygens. He believed that light is a special type of wave that propagates through a medium in the same way that sound travels through air. The medium for light, according to Huygens, was ether.

Since no one discovered the ether, and Newton's authority was huge at that time, Huygens' theory was rejected. However, in 1801, the Englishman Thomas Young conducted the following experiment: he passed monochromatic light through two narrow slits located close to each other. Passinghe projected the light onto the wall.
What was the result of this experience? If light were particles (corpuscles), as Newton believed, then the image on the wall would correspond to clear two bright bands coming from each of the slits. However, Jung observed a completely different picture. A series of dark and light stripes appeared on the wall, with light lines appearing even outside of both slits. A schematic representation of the described light pattern is shown in the figure below.
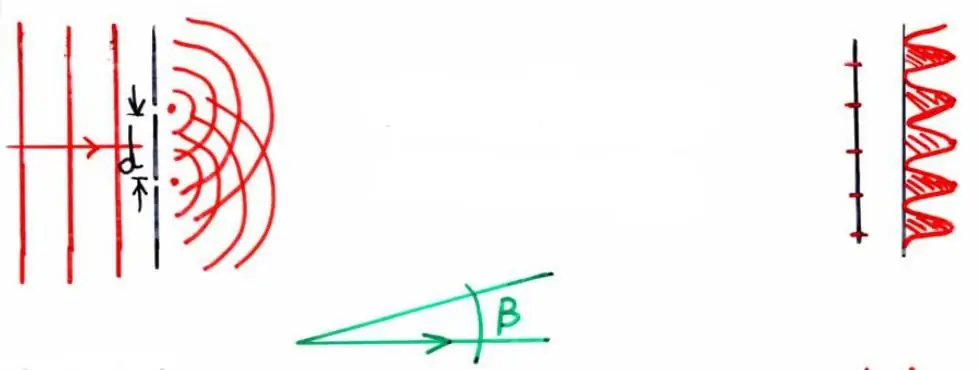
This picture said one thing: light is a wave.
Diffraction phenomenon
The light pattern in Young's experiments is connected with the phenomena of interference and diffraction of light. Both phenomena are difficult to separate from each other, since in a number of experiments their combined effect can be observed.
Diffraction of light consists in changing the wave front when it encounters an obstacle in its path, the dimensions of which are comparable to or less than the wavelength. From this definition it is clear that diffraction is characteristic not only for light, but also for any other waves, such as sound waves or waves on the surface of the sea.

It is also clear why this phenomenon cannot be observed in nature (the wavelength of light is several hundred nanometers, so any macroscopic objects cast clear shadows).
Huygens-Fresnel principle
The phenomenon of light diffraction is explained by the named principle. Its essence is as follows: a propagating rectilinear flatthe wave front leads to the excitation of secondary waves. These waves are spherical, but if the medium is homogeneous, then, superimposed on each other, they will lead to the original flat front.
As soon as any obstacle appears (for example, two gaps in Jung's experiment), it becomes a source of secondary waves. Since the number of these sources is limited and determined by the geometric features of the obstacle (in the case of two thin slots, there are only two secondary sources), the resulting wave will no longer produce the original flat front. The latter will change its geometry (for example, it will acquire a spherical shape), moreover, maxima and minima of the light intensity will appear in its different parts.
The Huygens-Fresnel principle demonstrates that the phenomena of interference and diffraction of light are inseparable.
What conditions are needed to observe diffraction?
One of them has already been mentioned above: it is the presence of small (of the order of the wavelength) obstacles. If the obstacle is of relatively large geometric dimensions, then the diffraction pattern will be observed only near its edges.
The second important condition for the diffraction of light is the coherence of waves from different sources. This means that they must have a constant phase difference. Only in this case, due to interference, it will be possible to observe a stable picture.
Coherence of sources is achieved in a simple way, it is enough to pass any light front from one source through one or more obstacles. Secondary sources from theseobstacles will already act as coherent.
Note that in order to observe the interference and diffraction of light, it is not at all necessary that the primary source be monochromatic. This will be discussed below when considering a diffraction grating.
Fresnel and Fraunhofer diffraction
In simple terms, Fresnel diffraction is the examination of the pattern on a screen located close to the slit. Fraunhofer diffraction, on the other hand, considers a pattern that is obtained at a distance much greater than the width of the slit, in addition, it assumes that the wavefront incident on the slit is flat.
These two types of diffraction are distinguished because the patterns in them are different. This is due to the complexity of the phenomenon under consideration. The fact is that in order to obtain an exact solution of the diffraction problem, it is necessary to use Maxwell's theory of electromagnetic waves. The Huygens-Fresnel principle, mentioned earlier, is a good approximation for obtaining practically usable results.
The figure below shows how the image in the diffraction pattern changes when the screen is moved away from the slit.

In the figure, the red arrow shows the direction of the screen approach to the slit, that is, the upper figure corresponds to Fraunhofer diffraction and the lower one to Fresnel. As you can see, as the screen approaches the slit, the picture becomes more complex.
Further in the article we will consider only Fraunhofer diffraction.
Diffraction by a thin slit (formulas)
As noted above,the diffraction pattern depends on the geometry of the obstacle. In the case of a thin slit of width a, which is illuminated with monochromatic light of wavelength λ, the position of the minima (shadow) can be observed for angles corresponding to the equality
sin(θ)=m × λ/a, where m=±1, 2, 3…
The angle theta here is measured from the perpendicular connecting the center of the slot and the screen. Thanks to this formula, it is possible to calculate at what angles the complete damping of the waves on the screen will occur. Moreover, it is possible to calculate the order of diffraction, that is, the number m.
Since we are talking about Fraunhofer diffraction, then L>>a, where L is the distance to the screen from the slit. The last inequality allows you to replace the sine of an angle with a simple ratio of the y coordinate to the distance L, which leads to the following formula:
ym=m×λ×L/a.
Here ym is the position coordinate of the minimum of order m on the screen.
Slit diffraction (analysis)
The formulas given in the previous paragraph allow us to analyze the changes in the diffraction pattern with a change in the wavelength λ or the slit width a. Thus, an increase in the value of a will lead to a decrease in the coordinate of the first-order minimum y1, that is, the light will be concentrated in a narrow central maximum. A decrease in the width of the slit will lead to a stretching of the central maximum, i.e., it becomes blurry. This situation is illustrated in the figure below.
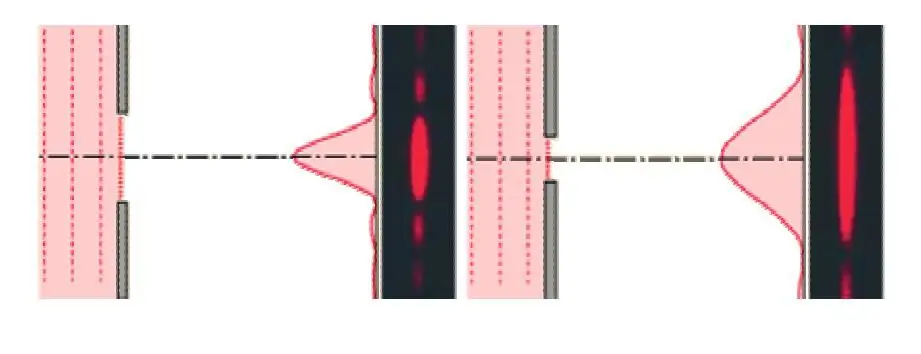
Changing the wavelength has the opposite effect. Large values of λlead to blurring of the picture. This means that long waves diffract better than short ones. The latter is of fundamental importance in determining the resolution of optical instruments.
Diffraction and resolution of optical instruments
The observation of the diffraction of light is the limiter of the resolution of any optical instrument, such as a telescope, microscope, and even the human eye. When it comes to these devices, they consider diffraction not by a slit, but by a round hole. Nevertheless, all the conclusions made earlier remain true.
For example, we will consider two luminous stars that are at a great distance from our planet. The hole through which light enters our eye is called the pupil. From two stars on the retina, two diffraction patterns are formed, each of which has a central maximum. If the light from the stars falls into the pupil at a certain critical angle, then both maxima will merge into one. In this case, a person will see a single star.
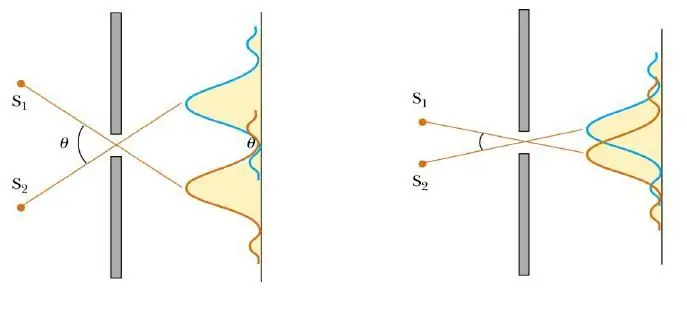
The resolution criterion was set by Lord J. W. Rayleigh, so it currently bears his surname. The corresponding mathematical formula looks like this:
sin(θc)=1, 22×λ/D.
Here D is the diameter of a round hole (lens, pupil, etc.).
Thus, the resolution can be increased (decrease θc) by increasing the lens diameter or decreasing the lengthwaves. The first variant is implemented in telescopes that make it possible to reduce θc by several times compared to the human eye. The second option, that is, reducing λ, finds application in electron microscopes, which have 100,000 times better resolution than similar light instruments.
Diffraction grating
It is a set of thin slots located at a distance d from each other. If the wave front is flat and falls parallel to this grating, then the position of the maxima on the screen is described by the expression
sin(θ)=m×λ/d, where m=0, ±1, 2, 3…
The formula shows that the zero-order maximum occurs in the center, the rest are located at some angles θ.
Since the formula contains the dependence of θ on the wavelength λ, this means that the diffraction grating can decompose light into colors like a prism. This fact is used in spectroscopy to analyze the spectra of various luminous objects.

Perhaps the most famous example of light diffraction is the observation of color shades on a DVD. The grooves on it are a diffraction grating, which, by reflecting light, decomposes it into a series of colors.






