To make it easier for the reader to imagine what a hyperboloid is - a three-dimensional object - you first need to consider the curved hyperbola of the same name, which fits into a two-dimensional space.
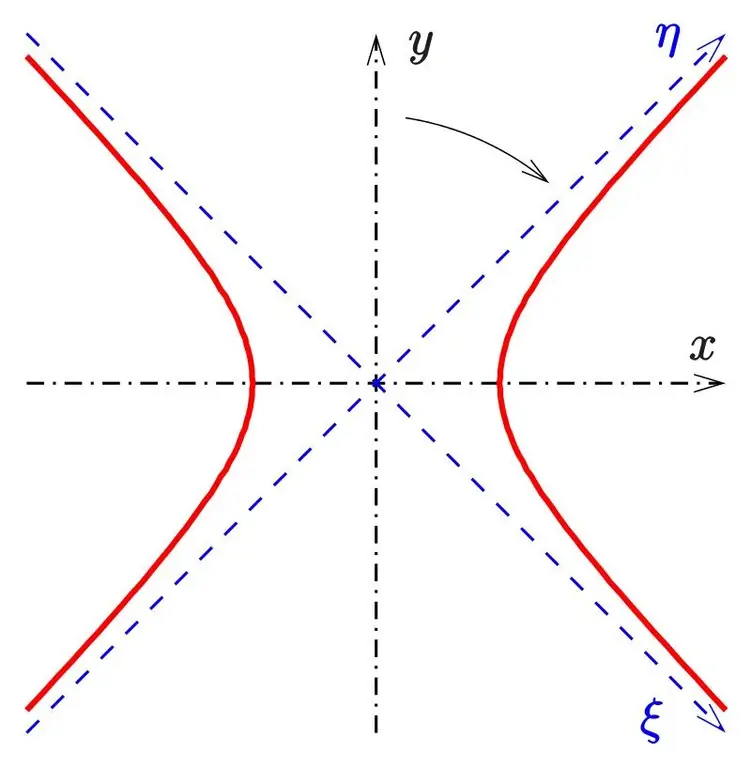
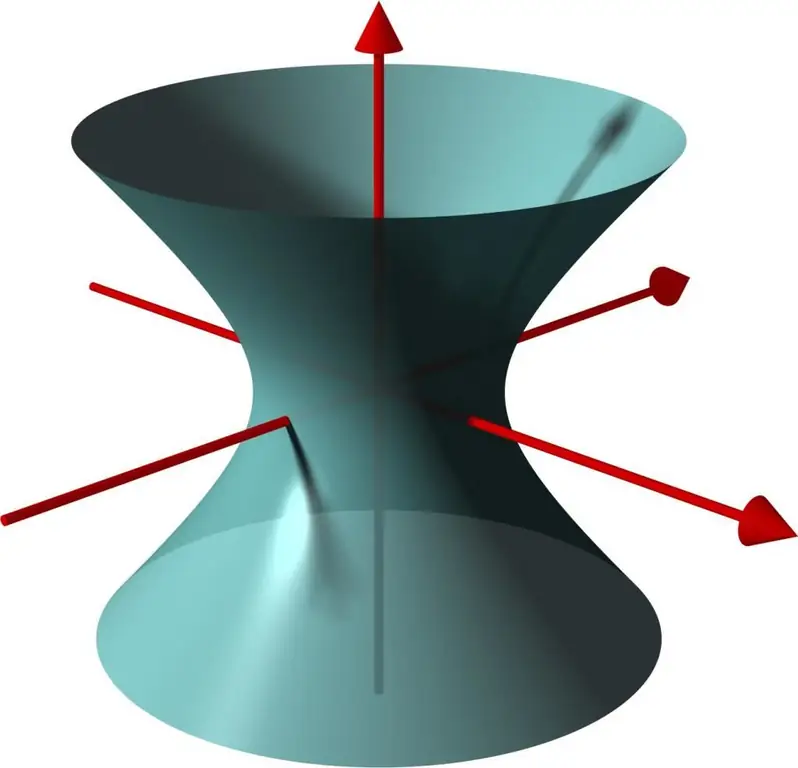
A hyperbola has two axes: the real one, which in this figure coincides with the abscissa axis, and the imaginary one, with the y-axis. If you mentally begin to turn the equation of a hyperbola around its imaginary axis, then the surface "seen" by the curve will be a single-sheeted hyperboloid.
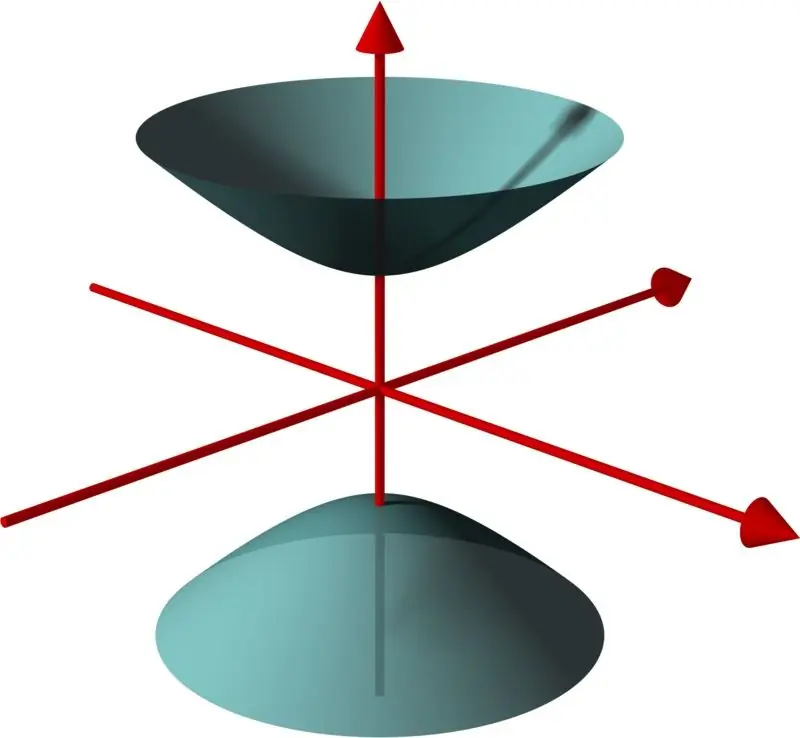
If, however, we begin to rotate the hyperbola around its real axis in this way, then each of the two "halves" of the curve will form its own separate surface, and together it will be called a two-sheeted hyperboloid.
Obtained by means of rotation of the corresponding plane curve, they are called, respectively, hyperboloids of rotation. They have parameters in all directions perpendicular to the axis of rotation,belonging to the rotated curve. In general, this is not the case.
Hyperboloid equation
In general, a surface can be defined by the following equations in Cartesian coordinates(x, y, z):

In the case of a hyperboloid of revolution, its symmetry about the axis around which it rotated is expressed in the equality of the coefficients a=b.
Hyperboloid characteristics
He has a trick. We know that curves on a plane have foci - in the case of a hyperbola, for example, the module of the difference in distances from an arbitrary point on a hyperbola to one focus and the second is constant by definition, in fact, of focus points.
When moving to three-dimensional space, the definition practically does not change: foci are again two points, and the difference in distances from them to an arbitrary point belonging to the hyperboloid surface is constant. As you can see, only the third coordinate appeared from the changes for all possible points, because now they are set in space. Generally speaking, defining a focus is equivalent to identifying the type of curve or surface: by talking about how the points of the surface are located relative to the foci, we actually answer the question of what a hyperboloid is and how it looks.
It is worth remembering that a hyperbola has asymptotes - straight lines, to which its branches tend to infinity. If, when constructing a hyperboloid of revolution, one mentally rotates the asymptotes together with the hyperbola, then in addition to the hyperboloid, one will also get a cone called asymptotic. The asymptotic cone isfor one-sheeted and two-sheeted hyperboloids.
Another important characteristic that only a one-sheeted hyperboloid has is rectilinear generators. As the name implies, these are lines, and they lie completely on a given surface. Two rectilinear generators pass through each point of a one-sheeted hyperboloid. They belong respectively to two families of lines, which are described by the following systems of equations:
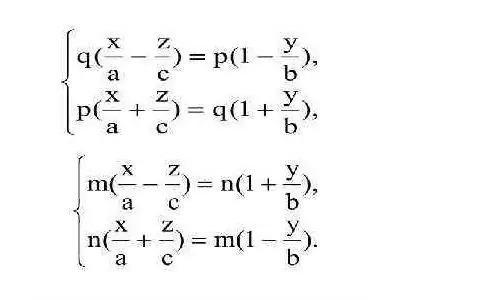
Thus, a one-sheeted hyperboloid can be entirely composed of an infinite number of straight lines of two families, and each line of one of them will intersect with all the lines of the other. Surfaces corresponding to such properties are called ruled; they can be constructed using the rotation of one straight line. Definition through the mutual arrangement of lines (rectilinear generators) in space can also serve as an unambiguous designation of what a hyperboloid is.
Interesting properties of a hyperboloid
Second-order curves and their corresponding surfaces of revolution each have interesting optical properties associated with foci. In the case of a hyperboloid, this is formulated as follows: if a ray is fired from one focus, then, having reflected from the nearest "wall", it will take such a direction as if it came from the second focus.
Hyperboloids in life
Most likely, most readers began their acquaintance with analytic geometry and second-order surfaces from a science fiction novel by Alexei Tolstoy"Hyperboloid engineer Garin". However, the writer himself either didn’t know well what a hyperboloid was, or sacrificed accuracy for the sake of artistry: the described invention, in terms of physical characteristics, is rather a paraboloid that collects all the rays in one focus (while the optical properties of the hyperboloid are associated with the scattering of rays).

The so-called hyperboloid structures are very popular in architecture: these are structures that are in shape a single-sheeted hyperboloid or a hyperbolic paraboloid. The fact is that only these surfaces of revolution of the second order have rectilinear generators: thus, a curved structure can only be built from straight beams. The advantages of such structures are in the ability to withstand heavy loads, for example, from the wind: the hyperboloid shape is used in the construction of tall structures, for example, television towers.






