Probability theory works with random variables. For random variables, there are so-called distribution laws. Such a law describes its random variable with absolute completeness. However, when working with real sets of random variables, it is often very difficult to immediately establish the law of their distribution and are limited to a certain set of numerical characteristics. For example, calculating the mean and variance of a random variable is often very useful.
Why is it needed
If the essence of the mathematical expectation is close to the mean value of the quantity, then in this case the dispersion tells how the values of our quantity are scattered around this mathematical expectation. For example, if we measured the IQ of a group of people and want to examine the measurement results (sample), the mathematical expectation will show the approximate average value of the intelligence quotient for this group of people, and if we calculate the sample variance, we will find out how the results are grouped around the mathematical expectation: a bunch near it (small spread in IQ) or more evenly over the entire area from the minimum to the maximum result (large spread, and somewhere in the middle - mathematical expectation).
To calculate the variance, a new characteristic of a random variable is needed - the deviation of the value from the mathematicalwaiting.
Deviation
To understand how to calculate the variance, you must first understand the deviation. Its definition is the difference between the value that a random variable takes and its mathematical expectation. Roughly speaking, in order to understand how a value is "scattered", you need to look at how its deviation is distributed. That is, we replace the value of the value with the value of its deviation from the mat. expectations and explore its distribution law.
The distribution law of a discrete, that is, a random variable that takes on individual values, is written in the form of a table, where the value of the value is correlated with the probability of its occurrence. Then, in the deviation distribution law, the random variable will be replaced by its formula, in which there is a value (which has retained its probability) and its own mat. waiting.
Properties of the law of distribution of the deviation of a random variable
We have written down the distribution law for the deviation of a random variable. From it, we can extract so far only such a characteristic as the mathematical expectation. For convenience, it is better to take a numerical example.
Let there be a distribution law for some random variable: X - value, p - probability.
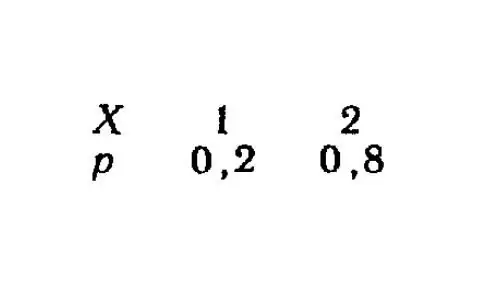
We calculate the mathematical expectation using the formula and immediately the deviation.

Drawing a new deviation distribution table.
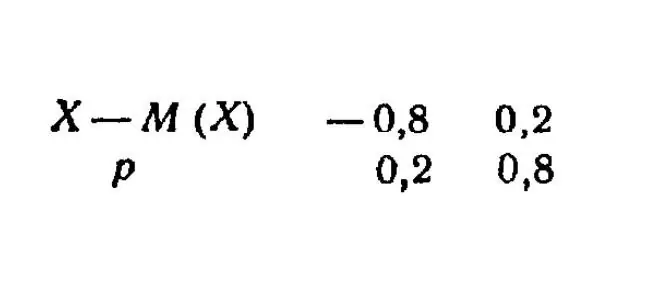
We calculate the expectation here as well.
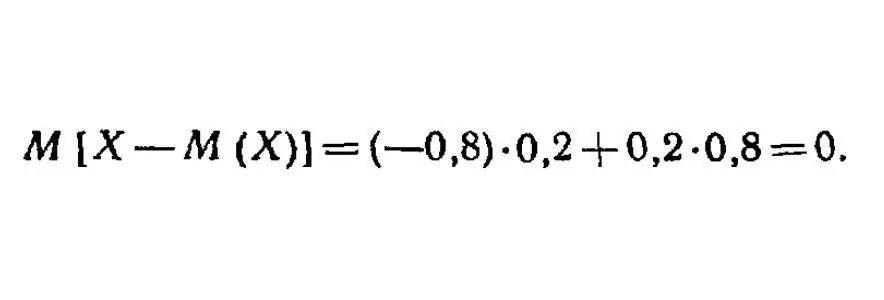
It turns out zero. There is only one example, but it will always be so: it is not difficult to prove this in the general case. The formula for the mathematical expectation of the deviation can be decomposed into the difference between the mathematical expectations of a random variable and, no matter how crooked it may sound, the mathematical expectation of the mat. expectations (recursion, however), which are the same, hence their difference will be zero.
This is expected: after all, deviations in sign can be both positive and negative, therefore, on average they should give zero.
How to calculate the variance of a discrete case. quantities
If mat. it is pointless to calculate the deviation expectation, you have to look for something else. You can simply take the absolute values of the deviations (modulo); but with modules, everything is not so simple, so the deviations are squared, and then their mathematical expectation is calculated. Actually, this is what is meant when they talk about how to calculate the variance.
That is, we take the deviations, square them, and make a table of squared deviations and probabilities that correspond to random variables. This is a new distribution law. To calculate the mathematical expectation, you need to add the products of the square of the deviation and the probability.
Easier formula
However, the article began with the fact that the law of distribution of the initial random variable is often unknown. So something lighter is needed. Indeed, there is another formula that allows you to calculate the sample variance using only the mat.waiting:
Dispersion - the difference between the mat. expectation of the square of a random variable and, conversely, the square of its mat. waiting.
There is a proof for this, but it does not make sense to present it here, since it has no practical value (and we only need to calculate the variance).
How to calculate the variance of a random variable in variation series
In real statistics, it is impossible to reflect all random variables (because, roughly speaking, there are, as a rule, an infinite number of them). Therefore, what gets into the study is the so-called representative sample from some general general population. And, since the numerical characteristics of any random variable from such a general population are calculated from the sample, they are called sample: sample mean, respectively, sample variance. You can calculate it in the same way as the usual one (through the squared deviations).
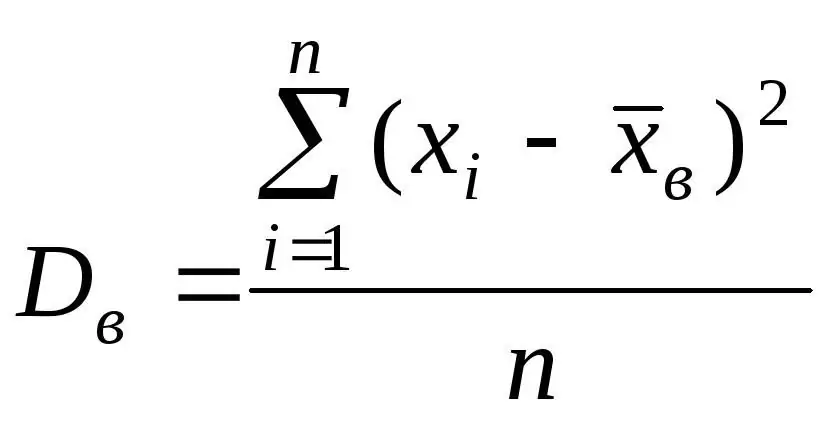
However, such a dispersion is called biased. The unbiased variance formula looks a little different. It is usually required to calculate it.
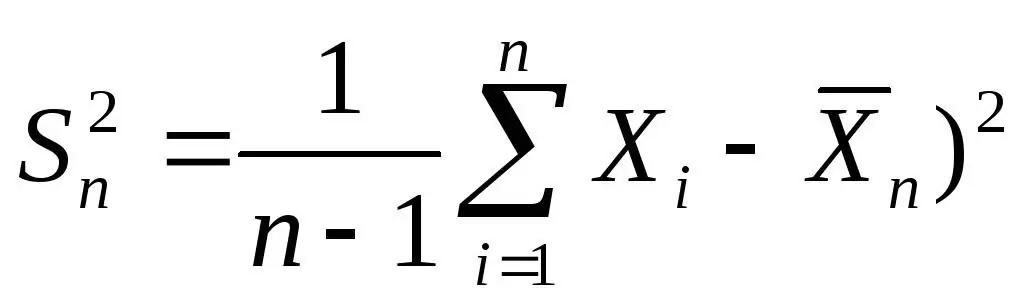
Small addition
One more numerical characteristic is connected with dispersion. It also serves to evaluate how the random variable scatters around its mat. expectations. There is not much difference in how to calculate the variance and standard deviation: the latter is the square root of the former.






