In physics, the consideration of problems with rotating bodies or systems that are in equilibrium is carried out using the concept of "moment of force". This article will consider the formula for the moment of force, as well as its use to solve this type of problem.
Moment of force in physics
As noted in the introduction, this article will focus on systems that can rotate either around an axis or around a point. Consider an example of such a model, shown in the figure below.
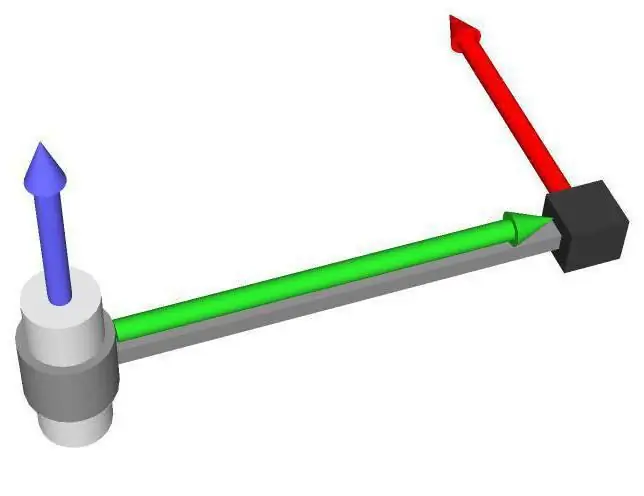
We see that the gray lever is fixed on the axis of rotation. At the end of the lever there is a black cube of some mass, on which a force acts (red arrow). It is intuitively clear that the result of this force will be the rotation of the lever around the axis counterclockwise.
The moment of force is a quantity in physics, which is equal to the vector product of the radius connecting the axis of rotation and the point of application of the force (green vector in the figure), and the external force itself. That is, the formula for the moment of force about the axis is writtenas follows:
M¯=r¯F¯
The result of this product is the vector M¯. Its direction is determined based on the knowledge of multiplier vectors, that is, r¯ and F¯. According to the definition of a cross product, M¯ must be perpendicular to the plane formed by the vectors r¯ and F¯, and directed in accordance with the right hand rule (if four fingers of the right hand are placed along the first multiplied vector towards the end of the second, then the thumb indicates where the desired vector is directed). In the figure, you can see where the vector M¯ is directed (blue arrow).
Scalar notation M¯
In the figure in the previous paragraph, the force (red arrow) acts on the lever at an angle of 90o. In the general case, it can be applied at absolutely any angle. Consider the image below.
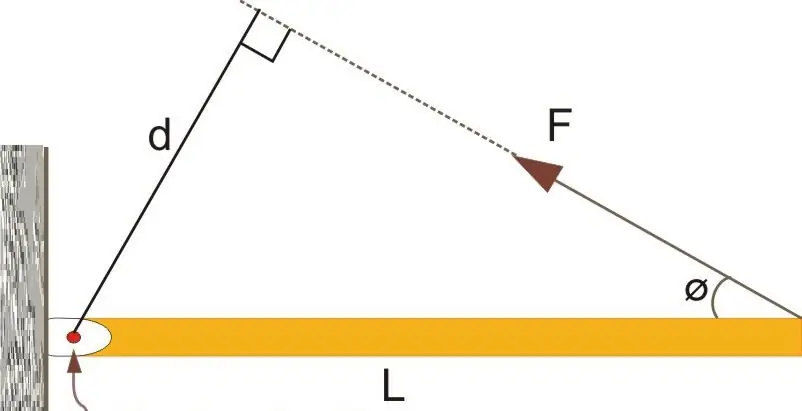
Here we see that the force F is already acting on the lever L at a certain angle Φ. For this system, the formula for the moment of force relative to a point (shown by an arrow) in scalar form will take the form:
M=LFsin(Φ)
It follows from the expression that the moment of force M will be the greater, the closer the direction of action of force F is to the angle 90o with respect to L. Conversely, if F acts along L, then sin(0)=0 and the force does not create any moment (M=0).
When considering the moment of force in scalar form, the concept of "lever of force" is often used. This value is the distance between the axis (pointrotation) and the vector F. Applying this definition to the figure above, we can say that d=Lsin(Φ) is the lever of force (the equality follows from the definition of the trigonometric function "sine"). Through the lever of force, the formula for the moment M can be rewritten as follows:
M=dF
Physical meaning of M
The considered physical quantity determines the ability of the external force F to exert a rotational effect on the system. To bring the body into rotational motion, it is necessary to inform it of some moment M.
A prime example of this process is opening or closing the door to a room. Holding the handle, the person makes an effort and turns the door on its hinges. Everyone can do it. If you try to open the door by acting on it near the hinges, then you will need to make great efforts to move it.
Another example is loosening a nut with a wrench. The shorter this key is, the more difficult it is to complete the task.
The indicated features are demonstrated by the formula of the moment of force over the shoulder, which was given in the previous paragraph. If M is considered a constant value, then the smaller d, the greater F must be applied to create a given moment of force.
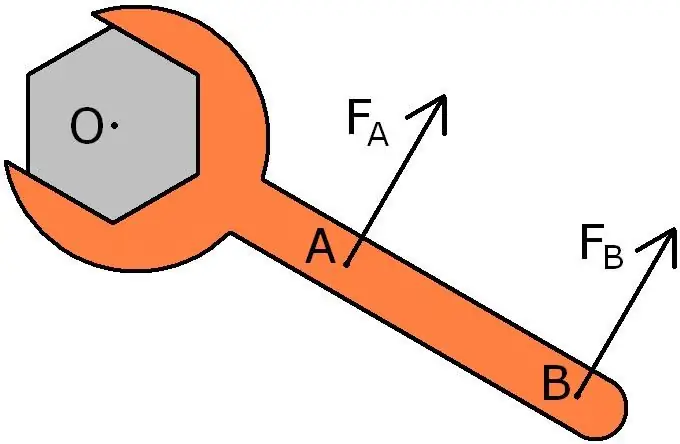
Several acting forces in the system
The cases were considered above when only one force F acts on a system capable of rotation, but what if there are several such forces? Indeed, this situation is more frequent, since forces can act on the systemdifferent nature (gravitational, electrical, friction, mechanical and others). In all these cases, the resulting moment of force M¯ can be obtained using the vector sum of all moments Mi¯, i.e.:
M¯=∑i(Mi¯), where i is the strength number Fi
From the property of the additivity of moments follows an important conclusion, which is called Varignon's theorem, named after the mathematician of the late 17th - early 18th century - the Frenchman Pierre Varignon. It reads: "The sum of the moments of all forces acting on the system under consideration can be represented as a moment of one force, which is equal to the sum of all the others and is applied to a certain point." Mathematically, the theorem can be written as follows:
∑i(Mi¯)=M¯=d∑i (Fi¯)
This important theorem is often used in practice to solve problems on the rotation and balance of bodies.

Does a moment of force do work?
Analyzing the above formulas in scalar or vector form, we can conclude that the value of M is some work. Indeed, its dimension is Nm, which in SI corresponds to the joule (J). In fact, the moment of force is not work, but only a quantity that is capable of doing it. For this to happen, it is necessary to have a circular motion in the system and a long-term action M. Therefore, the formula for the work of the moment of force is written as follows:
A=Mθ
BIn this expression, θ is the angle through which the rotation was made by the moment of force M. As a result, the unit of work can be written as Nmrad or Jrad. For example, a value of 60 Jrad indicates that when rotated by 1 radian (approximately 1/3 of the circle), the force F that creates the moment M did 60 joules of work. This formula is often used when solving problems in systems where friction forces act, as will be shown below.
Moment of force and moment of momentum
As shown, the impact of the moment M on the system leads to the appearance of rotational motion in it. The latter is characterized by a quantity called "momentum". It can be calculated using the formula:
L=Iω
Here I is the moment of inertia (a value that plays the same role in rotation as the mass in the linear motion of the body), ω is the angular velocity, it is related to the linear velocity by the formula ω=v/r.
Both moments (momentum and force) are related to each other by the following expression:
M=Iα, where α=dω / dt is the angular acceleration.
Let's give another formula that is important for solving problems for the work of moments of forces. Using this formula, you can calculate the kinetic energy of a rotating body. She looks like this:
Ek=1/2Iω2
Next, we present two problems with solutions, where we show how to use the considered physical formulas.
Equilibrium of several bodies
The first task is related to the equilibrium of a system in which several forces act. On theThe figure below shows a system that is acted upon by three forces. It is necessary to calculate what mass the object must be suspended from this lever and at what point it must be done so that this system is in balance.

From the condition of the problem, it can be understood that to solve it, one should use the Varignon theorem. The first part of the problem can be answered immediately, since the weight of the object to be hung from the lever will be:
P=F1 - F2 + F3=20 - 10 + 25=35 H
The signs here are chosen taking into account that the force that rotates the lever counterclockwise creates a negative moment.
Position of point d, where this weight should be hung, is calculated by the formula:
M1 - M2 + M3=dP=720 - 510 + 325=d35=> d=165/35=4, 714 m
Note that using the formula for the moment of gravity, we calculated the equivalent value M of the one created by three forces. In order for the system to be in equilibrium, it is necessary to suspend a body weighing 35 N at point 4, 714 m from the axis on the other side of the lever.
Moving disk problem
The solution of the following problem is based on the use of the formula for the moment of friction force and the kinetic energy of a body of revolution. Problem: Given a disk with a radius of r=0.3 meters, which rotates at a speed of ω=1 rad/s. It is necessary to calculate how far it can travel on the surface if the rolling friction coefficient is Μ=0.001.

This problem is easiest to solve if you use the law of conservation of energy. We have the initial kinetic energy of the disk. When it starts to roll, all this energy is spent on heating the surface due to the action of the friction force. Equating both quantities, we obtain the expression:
Iω2/2=ΜN/rrθ
The first part of the formula is the kinetic energy of the disk. The second part is the work of the moment of the friction force F=ΜN/r applied to the edge of the disk (M=Fr).
Given that N=mg and I=1/2mr2, we calculate θ:
θ=mr2 ω2/(4Μmg)=r 2 ω2/(4Μ g)=0, 32 1 2/(40.0019.81)=2.29358 rad
Since 2pi radians correspond to the length of 2pir, then we get that the required distance that the disk will cover is:
s=θr=2.293580.3=0.688m or about 69cm
Note that the mass of the disk does not affect this result.






