Rotation is a typical type of mechanical movement that is often found in nature and technology. Any rotation arises as a result of the action of some external force on the system under consideration. This force creates the so-called torque. What it is, what it depends on, is discussed in the article.
Rotation process
Before considering the concept of torque, let's characterize the systems to which this concept can be applied. The system of rotation assumes the presence in it of an axis around which a circular movement or rotation is carried out. The distance from this axis to the material points of the system is called the radius of rotation.
From the point of view of kinematics, the process is characterized by three angular values:
- rotation angle θ (measured in radians);
- angular velocity ω (measured in radians per second);
- angular acceleration α (measured in radians per square second).
These quantities are related to each other as followsequals:
ω=dθ/dt;
α=dω/dt.
Examples of rotation in nature are the movements of planets in their orbits and around their axes, the movements of tornadoes. In everyday life and technology, the movement in question is typical for engine motors, wrenches, building cranes, opening doors, and so on.
Determining the moment of force
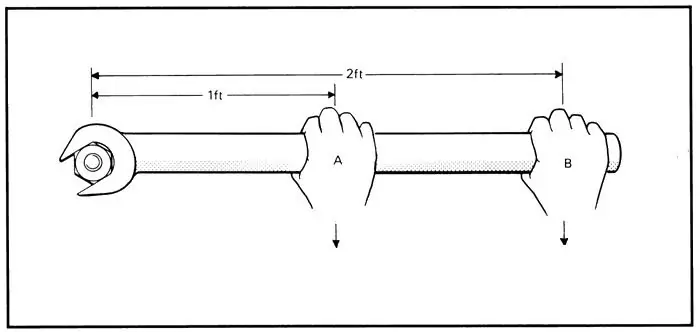
Now let's move on to the actual topic of the article. According to the physical definition, the moment of force is the vector product of the force application vector about the axis of rotation and the force vector itself. The corresponding mathematical expression can be written like this:
M¯=[r¯F¯].
Here the vector r¯ is directed from the axis of rotation to the point of application of the force F¯.
In this torque formula M¯, the force F¯ can be directed in any direction relative to the direction of the axis. However, the axis-parallel force component will not create rotation if the axis is rigidly fixed. In most problems in physics, one has to consider the forces F¯, which lie in planes perpendicular to the axis of rotation. In these cases, the absolute value of the torque can be determined by the following formula:
|M¯|=|r¯||F¯|sin(β).
Where β is the angle between vectors r¯ and F¯.
What is leverage?
The lever of force plays an important role in determining the magnitude of the moment of force. To understand what we are talking about, considernext picture.
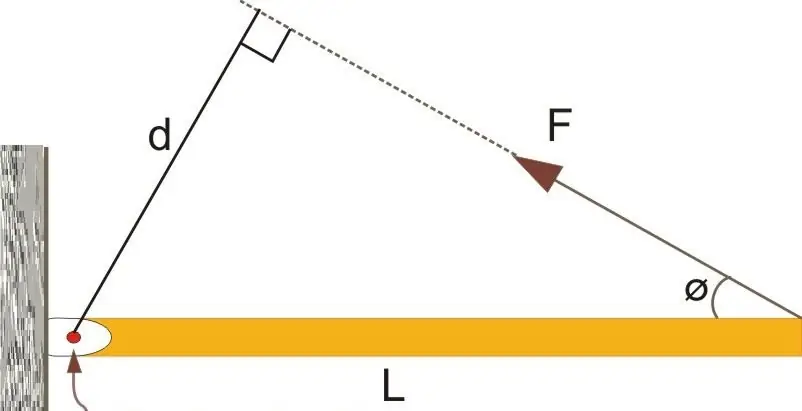
Here is shown a rod of length L, which is fixed at the pivot point by one of its ends. The other end is acted upon by a force F directed at an acute angle φ. According to the definition of the moment of force, one can write:
M=FLsin(180o-φ).
Angle (180o-φ) appeared because the vector L¯ is directed from the fixed end to the free end. Given the periodicity of the trigonometric sine function, we can rewrite this equality in the following form:
M=FLsin(φ).
Now let's pay attention to a right triangle built on sides L, d and F. By definition of the sine function, the product of the hypotenuse L and the sine of the angle φ gives the value of the leg d. Then we come to equality:
M=Fd.
The linear value d is called the lever of force. It is equal to the distance from the force vector F¯ to the axis of rotation. As can be seen from the formula, it is convenient to use the concept of a force lever when calculating the moment M. The resulting formula says that the maximum torque for some force F will occur only when the length of the radius vector r¯ (L¯ in the figure above) is equal to force lever, that is, r¯ and F¯ will be mutually perpendicular.
Direction of M¯
It was shown above that torque is a vector characteristic for a given system. Where is this vector directed? Answer this question nois especially difficult if we remember that the result of the product of two vectors is the third vector, which lies on an axis perpendicular to the plane of the original vectors.
It remains to decide whether the moment of force will be directed upwards or downwards (toward or away from the reader) relative to the said plane. You can determine this either by the gimlet rule, or by using the right hand rule. Here are both rules:
- Right hand rule. If you place the right hand in such a way that its four fingers move from the beginning of the vector r¯ to its end, and then from the beginning of the vector F¯ to its end, then the thumb, protruding, will indicate the direction of the moment M¯.
- Gimlet rule. If the direction of rotation of an imaginary gimlet coincides with the direction of rotational motion of the system, then the translational movement of the gimlet will indicate the direction of the vector M¯. Recall that it only rotates clockwise.
Both rules are equal, so everyone can use the one that is more convenient for him.
When solving practical problems, the different direction of the torque (up - down, left - right) is taken into account using the "+" or "-" signs. It should be remembered that the positive direction of the moment M¯ is considered to be the one that leads to the rotation of the system counterclockwise. Accordingly, if some force leads to the rotation of the system in the direction of the clock, then the moment created by it will have a negative value.
Physical meaningquantities M¯
In physics and mechanics of rotation, the value M¯ determines the ability of a force or a sum of forces to rotate. Since the mathematical definition of the quantity M¯ contains not only force, but also the radius vector of its application, it is the latter that largely determines the noted rotational ability. To make it clearer what ability we are talking about, here are a few examples:
- Every person, at least once in his life, tried to open the door, not by holding the handle, but by pushing it close to the hinges. In the latter case, you have to make a significant effort to achieve the desired result.
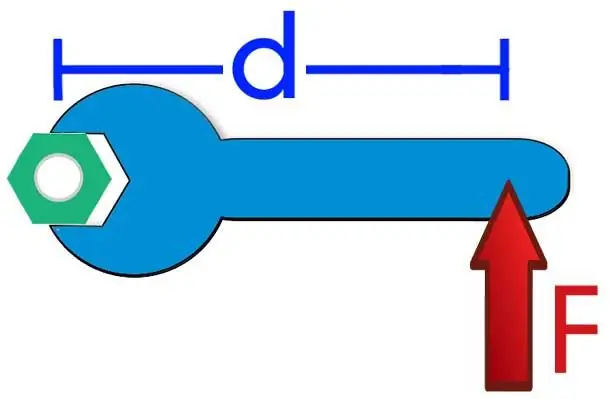
- To unscrew a nut from a bolt, use special wrenches. The longer the wrench, the easier it is to loosen the nut.
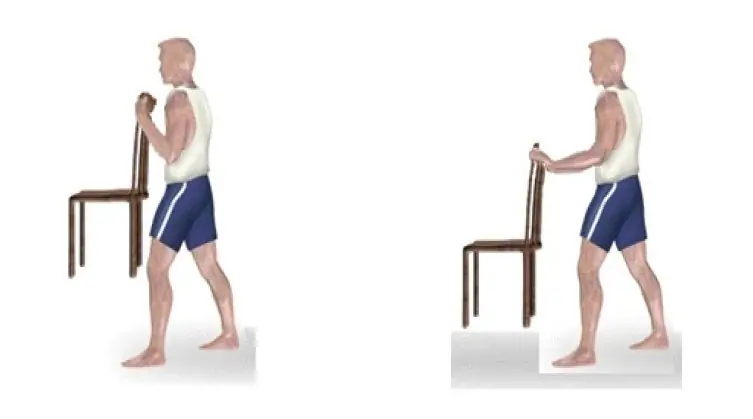
- To feel the importance of the lever of power, we invite readers to do the following experiment: take a chair and try to hold it with one hand on weight, in one case, lean the hand against the body, in the other, perform the task on a straight arm. The latter will prove to be an overwhelming task for many, although the weight of the chair has remained the same.
Units of moment of force
A few words should also be said about the SI units in which torque is measured. According to the formula written for it, it is measured in newtons per meter (Nm). However, these units also measure work and energy in physics (1 Nm=1 joule). The joule for moment M¯ does not apply because work is a scalar quantity, while M¯ is a vector.
Neverthelessthe coincidence of the units of the moment of force with the units of energy is not accidental. The work on the rotation of the system, done by the moment M, is calculated by the formula:
A=Mθ.
Where we get that M can also be expressed in joules per radian (J/rad).
Rotation dynamics
At the beginning of the article, we wrote down the kinematic characteristics that are used to describe the movement of rotation. In rotational dynamics, the main equation that uses these characteristics is:
M=Iα.
The action of the moment M on a system having a moment of inertia I leads to the appearance of an angular acceleration α.

This formula is used to determine the angular frequencies of rotation in engineering. For example, knowing the torque of an asynchronous motor, which depends on the frequency of the current in the stator coil and on the magnitude of the changing magnetic field, as well as knowing the inertial properties of the rotating rotor, it is possible to determine to what rotation speed ω the motor rotor spins in a known time t.
Example of problem solving
A weightless lever, 2 meters long, has a support in the middle. What weight should be put on one end of the lever so that it is in a state of equilibrium, if on the other side of the support at a distance of 0.5 meters from it lies a mass of 10 kg?

Obviously, the balance of the lever will come if the moments of forces created by the loads are equal in absolute value. The power that createsmoment in this problem, represents the weight of the body. The levers of force are equal to the distances from the weights to the support. Let's write the corresponding equality:
M1=M2=>
m1gd1=m2gd 2 =>
P2=m2g=m1gd 1/d2.
Weight P2 we get if we substitute from the condition of the problem the values m1=10 kg, d1=0.5 m, d2=1 m. The written equation gives the answer: P2=49.05 newtons.






