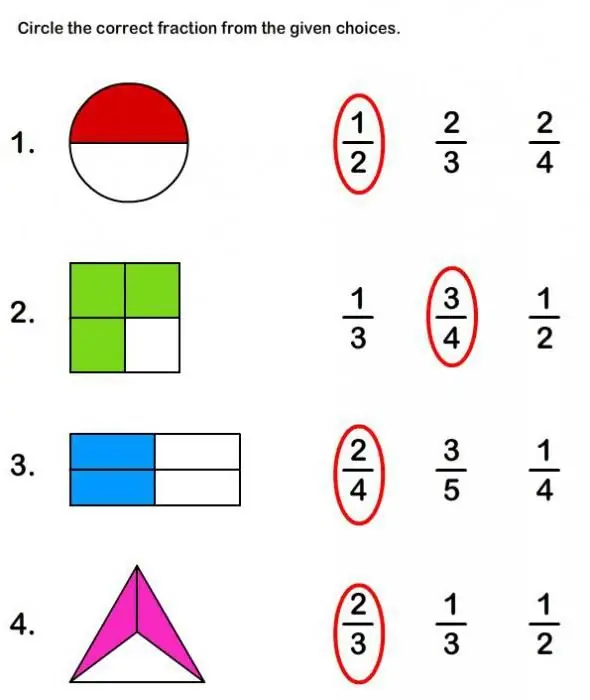
There comes a time when the teacher begins to explain what proper fractions are in math class. At this moment, a whole lot of new tasks and exercises open up before the student, for the implementation of which they have to “stretch themselves”. Not all students understand this topic the first time, but we will try to explain everything in an understandable language. After all, in fact, there is nothing complicated and scary here.
The meaning of the concept of "fraction"
At every step, a person encounters situations in which it is necessary to separate and connect objects and their parts. Whether we're chopping a log or cutting a cake, picking the bank with the highest percentages, or even looking at the time, right fractions are everywhere. It's basically just a fraction, a fragment - the top value tells us how many pieces we have, and the bottom one tells us how many it takes to get a whole value.
View from different points of view
Before you figure out how to make an improper fraction correct, you need to understand more fundamental issues. Namely, what is it all about?
Consider an example from everyday life. Take a pie, cut it into equal pieces - each of them will be, in fact, correctfraction, namely, a part of some whole. What happens if we add all the resulting fragments together? One whole pie. What if there are more parts than needed? We put the pieces together, resulting in a whole pie, plus some leftovers!

From a mathematical point of view, we got an improper fraction - this is when the parts add up to a value greater than one. Finding it in a problem or equation is easy. The lower part - the denominator - it has less than the upper part - the numerator. And if the lower number is greater than the upper one, then this is a proper fraction.
Use
For a person to want to study a subject or a specific topic, he must realize the practical value of new information. What are proper and improper fractions for? Where are they used? It is impossible to work with mathematical expressions without knowing fractions. And in other sciences, such information is indispensable: not in chemistry, not in physics, not in economics, not even in sociology or politics!
For example, they asked a group of people about a new candidacy for the country's president. Someone voted for one, and someone preferred the second, and on the TV screen we will see the percentage. What is a percentage? This is the correct fraction! In this case, the proportion of voters among a single set of respondents. In general, without fractions in this world - nowhere. So, you need to study them.
Mixed number
We already know what a proper fraction is. And the wrong one is one in which the numerator is greater than the denominator. It turns out that we have an integer and some additional part. Why not just write it down like this? This will be called a mixed number.
Imagine: the cake is cut into four parts, and in addition to them you have one more - the fifth. If you want to share with multiple friends, that's fine - you can just give each one a piece. But it’s more convenient to store the whole cake, isn’t it? It's the same in mathematics: it happens that it is more convenient to use the representation of a number as an improper fraction, and in other cases it is useful to single out integer parts in them - this will be called a mixed number.
Take 5/2 as an example. To get a mixed number, we need to subtract the denominator from the numerator as many times as it fits there. In this case, twice, and as a result we get two integers and one second. Such a transformation is the conversion of an improper fraction to a proper one. When instead of the wording "three second" we get the expression "one whole and one second", we come to the form as a mixed number.
Operations
With fractions, you can perform all the same operations as with integers: addition, subtraction, multiplication, division. Later you will learn how to raise to a power, extract square and cube roots, take logarithms. In the meantime, you need to learn how to perform simple operations with proper and improper fractions.
When multiplying and dividing, it is most convenient to use notmixed numbers, but the usual representation: only the numerator and denominator, without the integer part. So, we have two numbers and the sign of the operation between them - let it be this expression: (1/2)(2/3). And then everything, it turns out, is very simple: we multiply the upper and lower parts, and write the result through a fractional line: (12) / (23). We reduce the two in the numerator and denominator, getting the answer: 1/3.
When dividing, it will be almost the same, only the second component in the expression will “turn over”: (1/2) / (2/3)=(1/2)(3/2)=3/4.
Sum and difference
In addition and subtraction, you can use both mixed numbers and improper fractions with equal ease (if the need arises for the appropriate choice). To do this, you need to bring the terms to a common denominator.
How can this be done? If you remember the basic property of a fraction, then you know the answer - you need to multiply both fractions by such numbers so that they have the same values \u200b\u200bin the lower part. For example, there are the following values: 1/3 and 1/7. In accordance with the rule, we multiply the proper fraction 1/3 by 7, and 1/7 by 3. We get 7/21 and 3/21. Now the numbers can be freely added: (7+3)/21=10/21.
But multiplying by the neighboring denominator is not always necessary - if we had 1/4 and 1/8, it would be easier to multiply the first term by 2, and that's it: 2/8 + 1/8=3/8. The difference is calculated in the same way.
Mistakes
Students easily understand the topic of improper and proper fractions. What is itcomplex? If mistakes do happen, then almost always due to inattention - the common denominator is incorrectly found, for example. There is, of course, one popular mistake, and it is allowed in equations.

There is an expression: (3/4)x=3. It is required to find out what "x" is equal to. The error may lie in the fact that the student multiplies both sides of the equation by ¾, and not division. And then instead of the correct answer (x=4) it turns out to be incorrect: x=9/4. It is easy to get rid of this problem - you just need to take some time not to be lazy to write down the procedure for dividing the right and left parts. Then the error is immediately evident.
Record form
You can write fractions vertically or horizontally. In the first case, something similar to a column is obtained, where from top to bottom we get: the first number, a horizontal line, the second number. And if the line is narrow and it’s impossible to “swing” in height, then you can write these elements in a row, for example: 1/6, 34/37. Please note that such proper fractions are already written with a slash. Otherwise, nothing has changed significantly.
There are also decimal fractions. They are convenient to use, but not any number can be represented in this form - for this it must be divided by ten without a remainder, otherwise accuracy is lost. Look, ½ can be written in decimal form, getting 0.5, but 1/3 is no longer possible. Or rather, it will turn out 0, 333 … and so on ad infinitum. In mathematics, this is called "three in a period."
In a text editor
Is it possible to write down a fractionon the computer? "Word" provides such an opportunity. You just need to go to the "Insert" section. There you will see the "Formula" button, when clicked, a new window will open. In it you can find both proper fractions and many other, much more complex symbols - integrals, differentials, square roots.

You may not know these words yet, but one day you will pass them in mathematics too. Remember that all these signs can be found in one place.
At the same time, there is no such possibility in Notepad. There, fractions can only be written in a line, through a slash.
Conclusion
In any science, accuracy is important. Therefore, all the "pieces" must be taken into account, and for this it is imperative to understand how to work with regular and improper fractions. Without them, the plane won't take off, and the computer won't turn on, and you won't be able to cook a dish from a cookbook, and you won't even be able to write music. In general, understanding this topic in mathematics lessons is an absolutely necessary task, and most importantly, it is not at all difficult. Practice doing homework, adding, multiplying, comparing fractions. Then you will very quickly learn how to do everything in your mind and you can move on to new interesting topics. And believe me, there are still a great many of them in mathematics.






