Adiabatic transition between two states in gases is not one of the isoprocesses, however, it plays an important role not only in various technological processes, but also in nature. In this article, we will consider what this process is, and also give the adiabatic equations for an ideal gas.
Ideal gas in brief
An ideal gas is one in which there are no interactions between its particles, and their sizes are equal to zero. In nature, of course, there are no one hundred percent ideal gases, since they are all composed of molecules and atoms of size, which always interact with each other at least with the help of van der Waals forces. Nevertheless, the described model is often performed with sufficient accuracy for solving practical problems for many real gases.
The main equation of an ideal gas is the Clapeyron-Mendeleev law. It is written in the following form:
PV=nRT.
This equation establishes a direct proportionality between the productpressure P on the volume V and the amount of substance n on the absolute temperature T. The value of R is the gas constant, which plays the role of a proportionality factor.
What is an adiabatic process?
An adiabatic process is a transition between the states of a gas system in which there is no exchange of energy with the environment. In this case, all three thermodynamic characteristics of the system (P, V, T) change, and the amount of substance n remains constant.
Distinguish between adiabatic expansion and contraction. Both processes occur only due to the internal energy of the system. So, as a result of expansion, the pressure and especially the temperature of the system drop dramatically. Conversely, adiabatic compression results in a positive jump in temperature and pressure.
To prevent heat exchange between the environment and the system, the latter must have thermally insulated walls. In addition, shortening the process time significantly reduces heat flow to and from the system.
Poisson equations for an adiabatic process

The first law of thermodynamics is written as follows:
Q=ΔU + A.
In other words, the heat Q communicated to the system is used to perform work A by the system and to increase its internal energy ΔU. To write the adiabatic equation, one should put Q=0, which corresponds to the definition of the process under study. We get:
ΔU=-A.
With isochoricprocess in an ideal gas, all the heat goes to increase the internal energy. This fact allows us to write the equality:
ΔU=CVΔT.
Where CV is the isochoric heat capacity. Work A, in turn, is calculated as follows:
A=PdV.
Where dV is a small volume change.
In addition to the Clapeyron-Mendeleev equation, the following equation holds for an ideal gas:
CP- CV=R.
Where CP is the isobaric heat capacity, which is always greater than the isochoric one, since it takes into account gas losses due to expansion.
Analyzing the equations written above and integrating over temperature and volume, we arrive at the following adiabatic equation:
TVγ-1=const.
Here γ is the adiabatic index. It is equal to the ratio of isobaric heat capacity to isochoric. This equality is called the Poisson equation for an adiabatic process. Applying the Clapeyron-Mendeleev law, you can write two more similar expressions, only through the parameters P-T and P-V:
TPγ/(γ-1)=const;
PVγ=const.
Adiabatic graph can be given in different axes. Below it is shown in P-V axes.
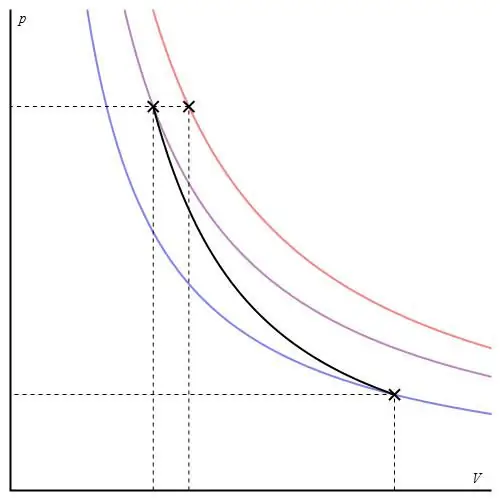
Colored lines on the graph correspond to isotherms, the black curve is an adiabat. As can be seen, the adiabat behaves more sharply than any of the isotherms. This fact is easy to explain: for the isotherm, the pressure changes backproportional to the volume, but for the isobath, the pressure changes faster, since the exponent is γ>1 for any gas system.
Example problem
In nature, in mountainous areas, when the air mass moves up the slope, its pressure drops, it increases in volume and cools. This adiabatic process lowers the dew point and produces liquid and solid precipitation.

It is proposed to solve the following problem: in the process of lifting the air mass along the slope of the mountain, the pressure dropped by 30% compared to the pressure at the foot. What was its temperature equal to if at the foot it was 25 oC?
To solve the problem, use the following adiabatic equation:
TPγ/(γ-1)=const.
It is better to write it in this form:
T2/T1=(P2/P 1)(γ-1)/γ.
If P1 is taken as 1 atmosphere, then P2 will be equal to 0.7 atmospheres. For air, the adiabatic index is 1.4, since it can be considered a diatomic ideal gas. The temperature value of T1 is 298.15 K. Substituting all these numbers into the expression above, we get T2=269.26 K, which corresponds to - 3, 9 oC.






