Studying the properties of an ideal gas is an important topic in physics. Introduction to the characteristics of gas systems begins with a consideration of the Boyle-Mariotte equation, since it is the first experimentally discovered law of an ideal gas. Let's consider it in more detail in the article.
What is meant by an ideal gas?
Before talking about the Boyle-Mariotte law and the equation that describes it, let's define an ideal gas. It is commonly understood as a fluid substance in which its constituent particles do not interact with each other, and their sizes are negligible in comparison with the average interparticle distances.
In fact, any gas is real, that is, its constituent atoms and molecules have a certain size and do not interact with each other with the help of van der Waals forces. However, at high absolute temperatures (more than 300 K) and low pressures (less than one atmosphere), the kinetic energy of atoms and molecules is much higher than the energy of van der Waals interactions, so the real gas at the indicatedconditions with high accuracy can be considered ideal.
Boyle-Mariotte Equation
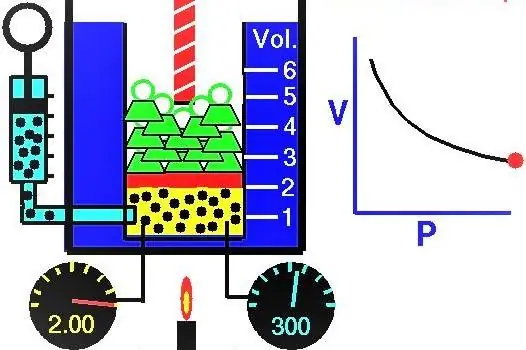
Properties of gases European scientists actively explored during the XVII-XIX centuries. The very first gas law that was discovered experimentally was the law describing the isothermal processes of expansion and compression of a gas system. Corresponding experiments were carried out by Robert Boyle in 1662 and Edm Mariotte in 1676. Each of these scientists independently showed that during an isothermal process in a closed gas system, pressure changes inversely with volume. The experimentally obtained mathematical expression of the process is written in the following form:
PV=k
Where P and V are the pressure in the system and its volume, k is some constant, the value of which depends on the amount of gas substance and its temperature. If you build the dependence of the P(V) function on a graph, then it will be a hyperbola. An example of these curves is shown below.
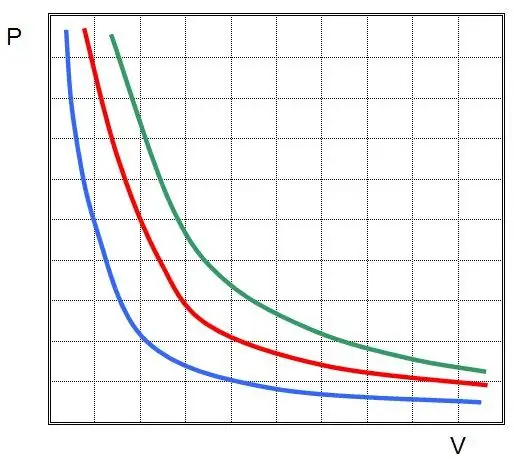
The written equality is called the Boyle-Mariotte equation (law). This law can be briefly formulated as follows: the expansion of an ideal gas at a constant temperature leads to a proportional decrease in pressure in it, on the contrary, isothermal compression of a gas system is accompanied by a proportional increase in pressure in it.
The ideal gas equation
Boyle-Mariotte law is a special case of a more general law that bears the names of Mendeleev andClapeyron. Emile Clapeyron, summarizing the experimental information on the behavior of gases under various external conditions, in 1834 obtained the following equation:
PV=nRT
In other words, the product of the volume V of a gas system and the pressure P in it is directly proportional to the product of the absolute temperature T and the amount of substance n. The coefficient of this proportionality is denoted by the letter R and is called the gas universal constant. In the written equation, the value of R appeared due to the replacement of a number of constants, which was made by Dmitry Ivanovich Mendeleev in 1874.
From the universal equation of state it is easy to see that the constancy of temperature and the amount of substance guarantees the invariance of the right side of the equation, which means that the left side of the equation will also remain constant. In this case, we get the Boyle-Mariotte equation.

Other gas laws
The Clapeyron-Mendeleev equation written in the paragraph above contains three thermodynamic parameters: P, V and T. If each of them is fixed, and the other two are allowed to change, then we get the Boyle-Mariotte, Charles and Gay-Lussac equations. Charles's law speaks of a direct proportionality between volume and temperature for an isobaric process, and Gay-Lussac's law states that in the case of an isochoric transition, the gas pressure increases or decreases in direct proportion to absolute temperature. The corresponding equations look like this:
V/T=const when P=const;
P/T=const when V=const.
SoThus, Boyle-Mariotte's law is one of the three main gas laws. However, it differs from the rest in terms of graphic dependence: the functions V(T) and P(T) are straight lines, the function P(V) is a hyperbola.
Example of a task for applying the Boyle-Mariotte law
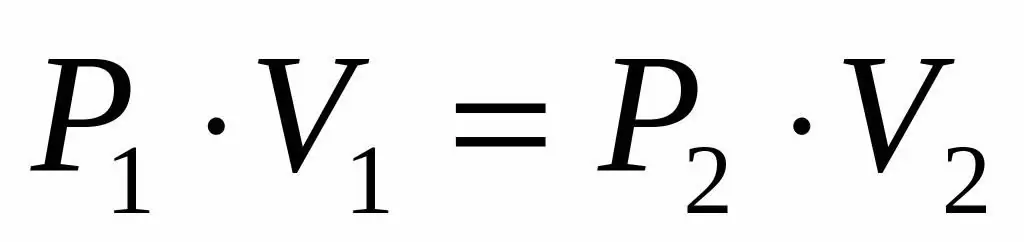
The volume of gas in the cylinder under the piston in the initial position was 2 liters, and its pressure was 1 atmosphere. What was the gas pressure equal to after the piston rose and the volume of the gas system increased by 0.5 liters. The process is considered isothermal.
Since we are given the pressure and volume of an ideal gas, and we also know that the temperature remains unchanged during its expansion, we can use the Boyle-Mariotte equation in the following form:
P1V1=P2V 2
This equality says that the volume product of pressure is constant for each state of the gas at a given temperature. Expressing the value P2 from equality, we obtain the final formula:
P2=P1V1/V 2
When doing pressure calculations, you can use off-system units in this case, because liters will shrink, and we get the pressure P2in atmospheres. Substituting the data from the condition, we arrive at the answer to the question of the problem: P2=0.8 atmospheres.






